【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论,其中正确结论是( )
A.b2<4ac
B.2a+b=0
C.a+b+c>0
D.若点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,则y1<y2
,y2)为函数图象上的两点,则y1<y2
参考答案:
【答案】D
【解析】解:A、∵由函数图象可知抛物线与x轴有2个交点,
∴b2﹣4ac>0即b2>4ac,故本题选项错误;
B、∵对称轴为直线x=﹣1,
∴﹣ ![]() =﹣1,即2a﹣b=0,故本选项错误;
=﹣1,即2a﹣b=0,故本选项错误;
C、∵抛物线与x轴的交点A坐标为(﹣3,0)且对称轴为x=﹣1,
∴抛物线与x轴的另一交点为(1,0),
∴将(1,0)代入解析式可得,a+b+c=0,故本选项错误;
D、∵抛物线的对称轴是直线x=﹣1,抛物线的开口向下,
∴当x>﹣1时,y随x的增大而减小,
∵﹣1< ![]() <
< ![]() ,点B(
,点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,
,y2)为函数图象上的两点,
∴y1<y2 , 故本选项正确;
故选D.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=
 ∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
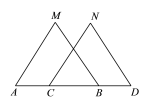
查看答案和解析>>【题目】如图,已知点A、C、B、D在同一条直线上,AC=BD,AM=CN,BM=DN,
求证:(1)△ABM ≌△CDN; (2)AM∥CN.
-
科目: 来源: 题型:
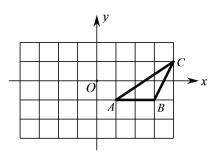
查看答案和解析>>【题目】如图,△ABC 顶点的坐标分别为 A (1,-1)、B(3,-1)、C(4,1).
⑴将△ABC向上平移1个单位,再向左平移1个单位,请画出平移后得到的△A1B1C1并写出点 A1、B1、C1 的坐标;
⑵若△A1B1C1 与△A1B1D 全等(D 点与 C1 不重合),直接写出点D的坐标.
-
科目: 来源: 题型:
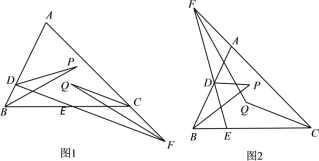
查看答案和解析>>【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
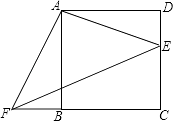
(1)填空:△ABF可以由△ADE绕旋转中心点 , 按逆时针方向旋转度得到;
(2)若BC=8,DE=6,求△AEF的面积.
相关试题

