【题目】(探索新知)如图1,点![]() 在线段
在线段![]() 上,图中共有3条线段:
上,图中共有3条线段:![]() 、
、![]() 、和
、和![]() ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点![]() 是线段
是线段![]() 的“二倍点”.
的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点![]() 表示数-10,点
表示数-10,点![]() 表示数20,若点
表示数20,若点![]() 从点
从点![]() ,以每秒3
,以每秒3![]() 的速度向点
的速度向点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时停止运动,设运动的时间为
时停止运动,设运动的时间为![]() 秒.
秒.
(2)点![]() 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含![]() 的代数式表示);
的代数式表示);
(3)求![]() 为何值时,点
为何值时,点![]() 是线段
是线段![]() 的“二倍点”;
的“二倍点”;
(4)同时点![]() 从点
从点![]() 的位置开始,以每秒2
的位置开始,以每秒2![]() 的速度向点
的速度向点![]() 运动,并与点
运动,并与点![]() 同时停止.请直接写出点
同时停止.请直接写出点![]() 是线段
是线段![]() 的“二倍点”时
的“二倍点”时![]() 的值.
的值.

参考答案:
【答案】(1)是 ;(2)![]() ;(3)
;(3)![]() 或5或
或5或![]() ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)可直接根据“二倍点”的定义进行判断;
(2)由题意可直接得出;
(3)用含t的代数式分别表示出线段AM、BM、AB,然后根据“二倍点”定义分类讨论的出结果;
(4)用含t的代数式分别表示出线段AN、MN、AM,然后根据“二倍点”定义分类讨论的出结果;
解:(1)因为线段的中点将线段分为相等的两部分,该线段等于2倍的中点一侧的线段长,符合“二倍点”的定义,所以一条线段的中点是这条线段的“二倍点”;
故答案为:是.
(2)由题意得出:
点![]() 在运动过程中表示的数为:20-3t
在运动过程中表示的数为:20-3t![]() ;
;
(3)AB=30,AM=30-3t,BM=3t,
当AM=2BM时,30-3t=6t,解得,![]() ;
;
当2AM=BM时,60-6t=3t,解得,![]() ;
;
当AM=BM时,30-3t=3t,解得,![]() ;
;
答:当![]() 或5或
或5或![]() 时,点
时,点![]() 是线段AB的“二倍点”.
是线段AB的“二倍点”.
(4)AN=2t,AM=30-3t,NM=5t-30,
当AN=2NM时2t=10t-60,解得,![]() ;
;
当2AM=NM时,60-6t=5t-30,解得,![]() ;
;
当AM=2NM时,30-3t=10t-60,解得,![]() .
.
答:当![]() 或
或![]() 或
或![]() 时,点
时,点![]() 是线段
是线段![]() 的“二倍点”.
的“二倍点”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
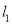 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 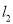 交于点
交于点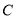 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(-1,0),B(3,0),将线段AB先向上平移
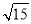 个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.(1)根据题意画出图形,直接写出C,D坐标;
(2)连接AD, 线段AD与
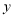 轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);(3)P(m,n)是坐标系内任一点,且
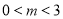 ,连接PC,PD,PO,PB,当
,连接PC,PD,PO,PB,当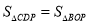 ,
,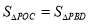 时,这样的点P存在吗?有几个?并求出点P的坐标.
时,这样的点P存在吗?有几个?并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上一点,
上一点, 为任一射线,
为任一射线, 平分
平分 ,
, 平分
平分 ,
,
(1)分别写出图中
 与
与 的补角;
的补角;(2)
 与
与 有怎样的数量关系,请说明理由.
有怎样的数量关系,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形; 若
若 ,
,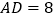 ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.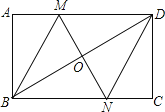
相关试题

