【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,根据三角形中位线定理得出OD∥BC,由DE⊥BC得出OD⊥DE,根据切线的判定定理即可得出结论;
(2)先证明Rt△CDB∽Rt△CED,然后根据相似三角形的对应边成比例求出BC的长,最后根据三角形的中位线定理即可求出圆的半径.
试题解析:
(1)证明:连接OD;
∵AD=CD,AO=BO,
∴OD∥BC.
∵DE⊥BC,
∴OD⊥DE.
∴DE与⊙O相切.
(2)连接BD,
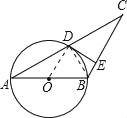
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∴∠BDC=90°,
又∵DE⊥BC,
Rt△CDB∽Rt△CED,
∴![]() =
=![]() ,
,
∴BC=![]() =
=![]()
又∵OD=![]() BC,
BC,
∴OD=![]() ×
×![]() =
=![]() ,
,
即⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一,抛物线
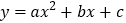 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线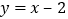 经过A、C两点,且
经过A、C两点,且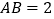 .
. 求抛物线的解析式;
求抛物线的解析式; 若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,
若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动, 如图
如图 ;当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设
;当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设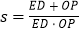 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.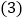 在
在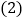 的条件下,是否存在t的值,使以P、B、D为顶点的三角形与
的条件下,是否存在t的值,使以P、B、D为顶点的三角形与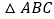 相似;若存在,求t的值;若不存在,请说明理由.
相似;若存在,求t的值;若不存在,请说明理由.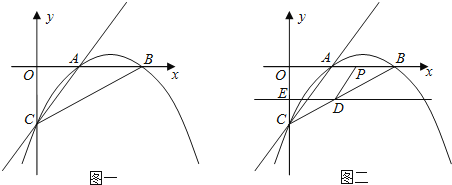
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度
人数
所占百分比
非常满意
12
10%
满意
54
m
比较满意
n
40%
不满意
6
5%

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
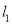 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 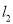 交于点
交于点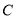 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)如图1,点
 在线段
在线段 上,图中共有3条线段:
上,图中共有3条线段: 、
、 、和
、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段
是线段 的“二倍点”.
的“二倍点”.(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点
 表示数-10,点
表示数-10,点 表示数20,若点
表示数20,若点 从点
从点 ,以每秒3
,以每秒3 的速度向点
的速度向点 运动,当点
运动,当点 到达点
到达点 时停止运动,设运动的时间为
时停止运动,设运动的时间为 秒.
秒.(2)点
 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含 的代数式表示);
的代数式表示);(3)求
 为何值时,点
为何值时,点 是线段
是线段 的“二倍点”;
的“二倍点”;(4)同时点
 从点
从点 的位置开始,以每秒2
的位置开始,以每秒2 的速度向点
的速度向点 运动,并与点
运动,并与点 同时停止.请直接写出点
同时停止.请直接写出点 是线段
是线段 的“二倍点”时
的“二倍点”时 的值.
的值.
相关试题

