【题目】如图,![]() 是直线
是直线![]() 上一点,
上一点,![]() 为任一射线,
为任一射线,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,

(1)分别写出图中![]() 与
与![]() 的补角;
的补角;
(2)![]() 与
与![]() 有怎样的数量关系,请说明理由.
有怎样的数量关系,请说明理由.
参考答案:
【答案】(1)∠AOF的补角是∠BOF和∠EOF;∠BOG的补角是∠AOG和∠EOG.
(2)![]() 与
与![]() 互余,理由见解析.
互余,理由见解析.
【解析】
(1)根据角平分线定义得出∠FOB=∠EOF,∠AOG=∠EOG,根据补角定义和邻补角定义求出即可.
(2)根据角平分线定义得出∠EOF=![]() ∠BOE,∠GOE=
∠BOE,∠GOE=![]() ∠AOE,根据∠AOE+∠BOE =180°,根据余角的定义得出即可.
∠AOE,根据∠AOE+∠BOE =180°,根据余角的定义得出即可.
解:(1)∵![]() 平分
平分![]() ,
,
∴∠FOB=∠EOF,
∵∠AOF+∠FOB=180°,
∴∠AOF的补角是∠BOF和∠EOF;
∵![]() 平分
平分![]() ,
,
∴∠AOG=∠EOG,
∵∠BOG+∠AOG=180°,
∴∠BOG的补角是∠AOG和∠EOG.
(2)![]() 与
与![]() 互余,
互余,
理由是:∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴∠EOF =![]()
![]() ,∠EOG=
,∠EOG=![]()
![]()
∴∠EOF+∠EOG=![]() (
(![]() +
+![]() )
)
∵![]() +
+![]() =180°,
=180°,
∴∠EOF+∠EOG=![]() =90°,
=90°,
∴![]() 与
与![]() 互余.
互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
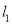 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 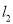 交于点
交于点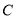 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)如图1,点
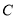 在线段
在线段 上,图中共有3条线段:
上,图中共有3条线段: 、
、 、和
、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段
是线段 的“二倍点”.
的“二倍点”.(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点
 表示数-10,点
表示数-10,点 表示数20,若点
表示数20,若点 从点
从点 ,以每秒3
,以每秒3 的速度向点
的速度向点 运动,当点
运动,当点 到达点
到达点 时停止运动,设运动的时间为
时停止运动,设运动的时间为 秒.
秒.(2)点
 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含 的代数式表示);
的代数式表示);(3)求
 为何值时,点
为何值时,点 是线段
是线段 的“二倍点”;
的“二倍点”;(4)同时点
 从点
从点 的位置开始,以每秒2
的位置开始,以每秒2 的速度向点
的速度向点 运动,并与点
运动,并与点 同时停止.请直接写出点
同时停止.请直接写出点 是线段
是线段 的“二倍点”时
的“二倍点”时 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(-1,0),B(3,0),将线段AB先向上平移
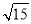 个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.(1)根据题意画出图形,直接写出C,D坐标;
(2)连接AD, 线段AD与
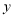 轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);(3)P(m,n)是坐标系内任一点,且
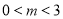 ,连接PC,PD,PO,PB,当
,连接PC,PD,PO,PB,当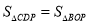 ,
,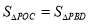 时,这样的点P存在吗?有几个?并求出点P的坐标.
时,这样的点P存在吗?有几个?并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;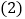 若
若 ,
,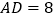 ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.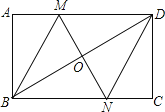
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
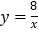 与一次函数
与一次函数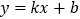 的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是
的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是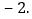 求:
求: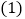 一次函数的解析式;
一次函数的解析式;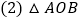 的面积;
的面积;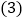 直接写出使反比例函数的值大于一次函数的值的x的取值范围.
直接写出使反比例函数的值大于一次函数的值的x的取值范围.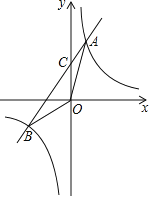
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
相关试题

