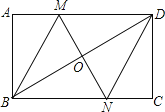
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:
(1)先由已知条件证四边形BMDN是平行四边形,结合MN垂直平分BD即可得到平行四边形BMDN是菱形;
(2)设BM=x,由四边形BMDN是菱形可得DM=BM=x,由此可得AM=AD-DM=8-x,这样在Rt△ABM中由勾股定理可求得x=5,这样由S菱形BMDN=MD·AB即可求出其面积了;在Rt△ABD中由已知易得BD=![]() ,结合S菱形BMDN=MD·AB=
,结合S菱形BMDN=MD·AB=![]() BD·MN即可求得MN的长.
BD·MN即可求得MN的长.
(1)∵四边形ABCD是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
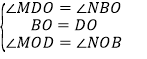 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形BMDN是平行四边形,
∵![]() ,
,
∴平行四边形BMDN是菱形.
(2)∵四边形BMDN是菱形,
∴![]() ,
,
设MD长为x,则![]() ,
,
在![]() 中,
中,![]()
即![]() ,
,
解得:![]() ,
,
即![]() .
.
菱形BMDN的面积![]() ,
,
∵![]() ,
,
又∵菱形BMDN的面积![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)如图1,点
 在线段
在线段 上,图中共有3条线段:
上,图中共有3条线段: 、
、 、和
、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段
是线段 的“二倍点”.
的“二倍点”.(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点
 表示数-10,点
表示数-10,点 表示数20,若点
表示数20,若点 从点
从点 ,以每秒3
,以每秒3 的速度向点
的速度向点 运动,当点
运动,当点 到达点
到达点 时停止运动,设运动的时间为
时停止运动,设运动的时间为 秒.
秒.(2)点
 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含 的代数式表示);
的代数式表示);(3)求
 为何值时,点
为何值时,点 是线段
是线段 的“二倍点”;
的“二倍点”;(4)同时点
 从点
从点 的位置开始,以每秒2
的位置开始,以每秒2 的速度向点
的速度向点 运动,并与点
运动,并与点 同时停止.请直接写出点
同时停止.请直接写出点 是线段
是线段 的“二倍点”时
的“二倍点”时 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(-1,0),B(3,0),将线段AB先向上平移
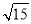 个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.(1)根据题意画出图形,直接写出C,D坐标;
(2)连接AD, 线段AD与
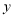 轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);(3)P(m,n)是坐标系内任一点,且
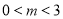 ,连接PC,PD,PO,PB,当
,连接PC,PD,PO,PB,当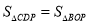 ,
,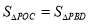 时,这样的点P存在吗?有几个?并求出点P的坐标.
时,这样的点P存在吗?有几个?并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上一点,
上一点, 为任一射线,
为任一射线, 平分
平分 ,
, 平分
平分 ,
,
(1)分别写出图中
 与
与 的补角;
的补角;(2)
 与
与 有怎样的数量关系,请说明理由.
有怎样的数量关系,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
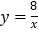 与一次函数
与一次函数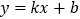 的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是
的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是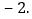 求:
求: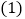 一次函数的解析式;
一次函数的解析式;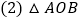 的面积;
的面积; 直接写出使反比例函数的值大于一次函数的值的x的取值范围.
直接写出使反比例函数的值大于一次函数的值的x的取值范围.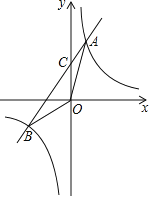
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
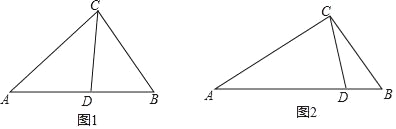
查看答案和解析>>【题目】经过三边都不相等的三角形的一个顶点的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线
(2)在△ABC中,∠A=52°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=3,BC=2,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
相关试题

