【题目】在平面直角坐标系中,A(-1,0),B(3,0),将线段AB先向上平移![]() 个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
(1)根据题意画出图形,直接写出C,D坐标;
(2)连接AD, 线段AD与![]() 轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
(3)P(m,n)是坐标系内任一点,且![]() ,连接PC,PD,PO,PB,当
,连接PC,PD,PO,PB,当![]() ,
,![]() 时,这样的点P存在吗?有几个?并求出点P的坐标.
时,这样的点P存在吗?有几个?并求出点P的坐标.
参考答案:
【答案】(1)图形见解析,![]() ;(2)点E(0,
;(2)点E(0,![]() );(3)这样的P点只有一个,即
);(3)这样的P点只有一个,即![]()
【解析】
(1)根据平移的性质画出图形,即可得到C,D坐标;
(2)先证四边形ABDC为菱形,结合菱形的性质及勾股定理求E点的坐标.
(3)分三种情况讨论:①P点在四边形OBDC内部 ②P在CD上方 ③P在AB下方
(1)如图,![]()
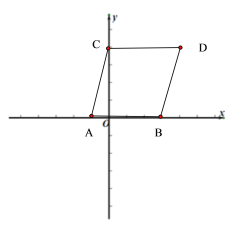
(2)![]() ,
,
∴四边形ABDC是平行四边形
又由勾股定理得:![]()
![]()
∴平行四边形ABCD为菱形
连接EB,如下图:设![]()
∵在菱形ABDC中,AD是BC的中垂线,
![]()
在Rt△OBE中,由勾股定理得: ![]()
解得:![]()
所以点E(0,![]() )
)
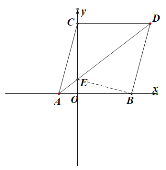
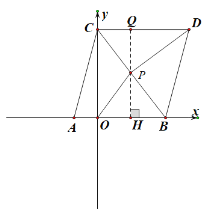
(3)①P点在四边形OBDC内部,如下图:
过P点作PH⊥OB于H,反向延长PH交CD于Q
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
∴![]()
②P在CD上方,如下图
过P作PJ⊥OB于J,与CD交于K,
同①理得PK⊥CD
![]() ,
,![]()
依题意得![]() 解得
解得![]()
![]()
![]()
依题意得![]() ,解得
,解得![]() >3(舍)
>3(舍)

③P在AB下方,![]() ∴与条件不符,舍去
∴与条件不符,舍去
综上所述,这样的P点只有一个,即![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
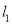 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 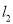 交于点
交于点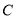 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)如图1,点
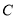 在线段
在线段 上,图中共有3条线段:
上,图中共有3条线段: 、
、 、和
、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点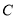 是线段
是线段 的“二倍点”.
的“二倍点”.(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点
 表示数-10,点
表示数-10,点 表示数20,若点
表示数20,若点 从点
从点 ,以每秒3
,以每秒3 的速度向点
的速度向点 运动,当点
运动,当点 到达点
到达点 时停止运动,设运动的时间为
时停止运动,设运动的时间为 秒.
秒.(2)点
 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含 的代数式表示);
的代数式表示);(3)求
 为何值时,点
为何值时,点 是线段
是线段 的“二倍点”;
的“二倍点”;(4)同时点
 从点
从点 的位置开始,以每秒2
的位置开始,以每秒2 的速度向点
的速度向点 运动,并与点
运动,并与点 同时停止.请直接写出点
同时停止.请直接写出点 是线段
是线段 的“二倍点”时
的“二倍点”时 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上一点,
上一点, 为任一射线,
为任一射线, 平分
平分 ,
, 平分
平分 ,
,
(1)分别写出图中
 与
与 的补角;
的补角;(2)
 与
与 有怎样的数量关系,请说明理由.
有怎样的数量关系,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形; 若
若 ,
,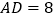 ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.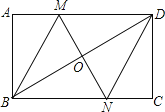
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
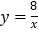 与一次函数
与一次函数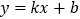 的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是
的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是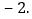 求:
求: 一次函数的解析式;
一次函数的解析式;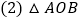 的面积;
的面积; 直接写出使反比例函数的值大于一次函数的值的x的取值范围.
直接写出使反比例函数的值大于一次函数的值的x的取值范围.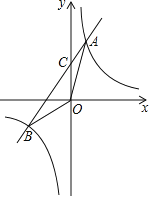
相关试题

