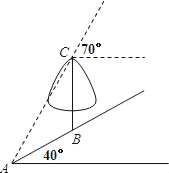
【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
参考答案:
【答案】树影AB的长约为2.7米.
【解析】试题分析:本题可通过构造直角三角形来解答,过B点作BD⊥AC,D为垂足,在直角三角形BCD中,已知BC的长,可求∠BCD的度数,那么可求出BD的长,在直角三角形ABD中,可求∠DAB=70°-40°=30°,前面又得到了BD的长,那么就可求出AB的长.
试题解析:过B点作BD⊥AC,D为垂足,
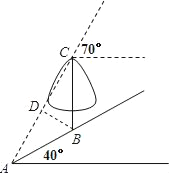
在直角三角形BCD中,∠BCD=180°﹣70°﹣90°=20°,
BD=BCsin20°=4×0.34=1.36米,
在直角三角形ABD中,∠DAB=70°﹣40°=30°,
AB=BD÷sin30°=1.36÷![]() ≈2.7米.
≈2.7米.
答:树影AB的长约为2.7米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在
 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.(1)求证:CF⊥AB;
(2)若CD=4,CB=4
 ,cos∠ACF=
,cos∠ACF= ,求EF的长.
,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 的顶点
的顶点 、
、 在
在 轴上,顶点
轴上,顶点 在
在 轴上,已知
轴上,已知 ,
, ,
, .
.
(1)平行四边形
 的面积为________;
的面积为________;(2)如图1,点
 是
是 边上的一点,若
边上的一点,若 的面积是平行四边形
的面积是平行四边形 的
的 ,求点
,求点 的坐标;
的坐标;(3)如图2,将
 绕点
绕点 顺时针旋转,旋转得
顺时针旋转,旋转得 ,在整个旋转过程中,能否使以点
,在整个旋转过程中,能否使以点 、
、 、
、 、
、 为顶点的四边形是平行四边形?若能,求点
为顶点的四边形是平行四边形?若能,求点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月23日,第24个世界读书日,为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为每个班级订购了一批新的图书,初一年级两个班订购图书情况如下表:

老舍文集(套)
四大名善(套)
总表用(元)
初一(1)班
4
2
80
初一(2)班
2
3
520
(1)求老舍文集和四大名著每套各是多少元;
(2)学校准备再购买老舍文集和四大名著共10套,总费用不超过700元。问学校有哪几种购买方案。
-
科目: 来源: 题型:
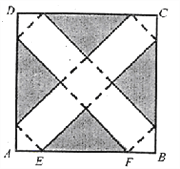
查看答案和解析>>【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别在矩形ABCD的边AD、AB上,连接EF,四边形ABFE沿EF翻折能与四边形
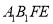 重合,且
重合,且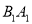 与ED相交,若
与ED相交,若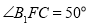 ,则
,则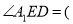
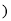
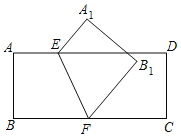
A.
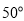 B.
B. 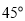 C.
C.  D.
D. 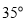
相关试题

