【题目】如图,平行四边形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,已知
轴上,已知![]() ,
,![]() ,
,![]() .
.

(1)平行四边形![]() 的面积为________;
的面积为________;
(2)如图1,点![]() 是
是![]() 边上的一点,若
边上的一点,若![]() 的面积是平行四边形
的面积是平行四边形![]() 的
的![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将![]() 绕点
绕点![]() 顺时针旋转,旋转得
顺时针旋转,旋转得![]() ,在整个旋转过程中,能否使以点
,在整个旋转过程中,能否使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若能,求点
为顶点的四边形是平行四边形?若能,求点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
参考答案:
【答案】(1)32;(2)点E的坐标为(![]() ,2);(3)能,点A1的坐标为
,2);(3)能,点A1的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由题意可得AB=8,根据平行四边形的面积公式可求得ABCD的面积;
(2)过点E作EF⊥AB,根据△ABE的面积是ABCD的![]() ,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
(3)分以下三种情况讨论:①四边形OA1D1B是平行四边形,②四边形A1D1OB是平行四边形,③四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E.先分别画出示意图,利用旋转的性质,平行四边形的性质再结合面积法及勾股定理可分别得出点A1的坐标.
解:(1)∵OA=3,OB=5,OD=4.
∴AB=8,∴ABCD的面积=4×8=32,
故答案为:32;
(2)过点E作EF⊥AB于F,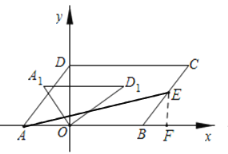
∵S△ABE=![]() SABCD,∴
SABCD,∴![]() ×AB×EF=
×AB×EF=![]() ×32,∴EF=2.
×32,∴EF=2.
∵OB=5,CD=AB=8,OD=4,
∴点B(5,0),点C(8,4),
设直线BC的解析式为y=kx+b,
![]() ,解得
,解得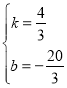 ,
,
∴直线BC的解析式为y=![]() ,
,
当y=2时,x=![]() ,
,
∴点E的坐标为(![]() ,2);
,2);
(3)能使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,理由如下:
为顶点的四边形是平行四边形,理由如下:
∵OA=3,OD=4,∴AD=5,分以下三种情况:
①如图,若四边形OA1D1B是平行四边形,A1D1交y轴于点F,
∵将△AOD绕点O顺时针旋转,旋转得△A1OD1,
∴A1O=AO=3,OD1=OD=4,∠A1OD1=∠AOD=90°.
∵四边形OA1D1B是平行四边形,
∴A1D1=BO=5,A1D1∥AB,∴∠A1FO=180°-∠AOD=90°,
∴S△A1OD1=![]() ×A1O×OD1=
×A1O×OD1=![]() ×A1D1×OF,
×A1D1×OF,
∴OF=![]() ,
,![]() ,
,
∵点A1在第二象限,∴A1的坐标为![]() ;
;
②如图,若四边形A1D1OB是平行四边形,A1D1交y轴于点F,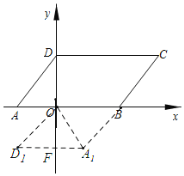
同①可得,![]() ,
,
∵点A1在第四象限,∴A1的坐标为![]() ;
;
③如图,若四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E,
∵OA1BD1是平行四边形,且∠A1OD1=90°,
∴四边形OA1BD1是矩形,∴OD1=A1B=4,∠OA1B=90°,
∵S△A1OB=![]() ×OB×A1E=
×OB×A1E=![]() ×A1O×A1B,
×A1O×A1B,
∴A1E=![]() ,∴OE=
,∴OE=![]() ,
,
∴A1的坐标为![]() .
.
综上所述,符合条件的点A1的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A. b≥
 B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2
B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在
 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.(1)求证:CF⊥AB;
(2)若CD=4,CB=4
 ,cos∠ACF=
,cos∠ACF= ,求EF的长.
,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

-
科目: 来源: 题型:
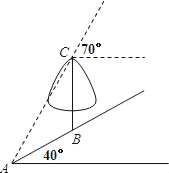
查看答案和解析>>【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月23日,第24个世界读书日,为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为每个班级订购了一批新的图书,初一年级两个班订购图书情况如下表:

老舍文集(套)
四大名善(套)
总表用(元)
初一(1)班
4
2
80
初一(2)班
2
3
520
(1)求老舍文集和四大名著每套各是多少元;
(2)学校准备再购买老舍文集和四大名著共10套,总费用不超过700元。问学校有哪几种购买方案。
相关试题

