搜索
【题目】某地居民生活用电基本价格为每度电0.4元，若每月用电量不超过
度时，按基本价格收费；若超过度，超出部分按基本价格的150%收费.
（1）某户8月份用电84度，共交电费38.4元，求的值。
（2）如果该户9月份的电费平均为每度0.5元，那么该用户9月份用电多少度？应交电费多少元？
参考答案：
【答案】该用户9月份用电120度，应交电费60元
【解析】
（1）根据题意可知8月份用电84度，电费的计算方法为：0.40x+（84-x）×0.40×150%由此即可列方程，解方程即可解决；（2）设该户9月份用电
度，电费的计算两种方法为：①0.40x+（y-x）×0.40×150%，②
由此即可列方程，解方程求解即可．
（1）
（2）设该户9月份用电度，依题意得：
（元）
答：该用户9月份用电120度，应交电费60元。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．
（1）当AN平分∠MAB时，求DM的长；
（2）连接BN，当DM=1时，求△ABN的面积；
（3）当射线BN交线段CD于点F时，求DF的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，抛物线y=ax2+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．
（1）当h=1，k=2时，求抛物线的解析式；
（2）若抛物线y=tx2（t≠0）也经过A点，求a与t之间的关系式；
（3）当点A在抛物线y=x2﹣x上，且﹣2≤h＜1时，求a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A，B两点，点A在点B的左侧．
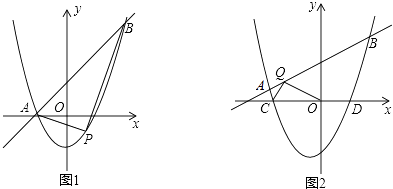
（1）如图1，当k=1时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），在直线y=kx+1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】公园门票价格规定如下表：
某校七年级（1）、（2）两个班104人去游园，其中七（1）班不足50人，（2）班超过50人，但不足100人。经估算，如果两个班都以班为单位购票，则一共应付1240元。问：
（1）两班各有多少学生？
（2）如果两班联合起来，作为一个团体购票，可省多少钱？
（3）如果七（1）班单独组织去游园，作为组织者的你将如何购票才最省钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上，∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC．
（1）试判断BE与FH的数量关系，并说明理由；
（2）求证：∠ACF=90°；
（3）连接AF，过A、E、F三点作圆，如图2，若EC=4，∠CEF=15°，求
的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】两种移动电话计费方式表如下：
（1）设一个月内在本地通话时间为
分钟，全球通收费表示为 元，神州行收费表示为 元（2）若某用户一个月内本地通话时间为2.5小时，你认为选择哪种方式较为划算？
（3）当通话时间为多少时间，两种收费方式的费用是一样的？
相关试题
