【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
参考答案:
【答案】
(1)
由折叠性质得:△ANM≌△ADM,
∴∠MAN=∠DAM,
∵AN平分∠MAB,∠MAN=∠NAB,
∴∠DAM=∠MAN=∠NAB,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DAM=30°,
∴DM=ADtan∠DAM=3×tan30°=3× ![]() =
= ![]()
(2)
延长MN交AB延长线于点Q,如图1所示:

∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAQ,
由折叠性质得:△ANM≌△ADM,
∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,
∴∠MAQ=∠AMQ,
∴MQ=AQ,
设NQ=x,则AQ=MQ=1+x,
∵∠ANM=90°,
∴∠ANQ=90°,
在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2,
∴(x+1)2=32+x2,
解得:x=4,
∴NQ=4,AQ=5,
∵AB=4,AQ=5,
∴S△NAB= ![]() S△NAQ=
S△NAQ= ![]() ×
× ![]() ANNQ=
ANNQ= ![]() ×
× ![]() ×3×4=
×3×4= ![]() ;
;
(3)
过点A作AH⊥BF于点H,如图2所示:

∵四边形ABCD是矩形,
∴AB∥DC,
∴∠HBA=∠BFC,
∵∠AHB=∠BCF=90°,
∴△ABH∽△BFC,
∴ ![]() ,
,
∵AH≤AN=3,AB=4,
∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:

由折叠性质得:AD=AH,
∵AD=BC,
∴AH=BC,
在△ABH和△BFC中, 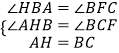 ,
,
∴△ABH≌△BFC(AAS),
∴CF=BH,
由勾股定理得:BH= ![]() =
= ![]() =
= ![]() ,
,
∴CF= ![]() ,
,
∴DF的最大值=DC﹣CF=4﹣ ![]()
【解析】(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=ADtan∠DAM= ![]() 即可;(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例
即可;(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例 ![]() =
= ![]() ,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,熟练掌握矩形和折叠的性质,证明三角形相似和三角形全等是解决问题的关键.
,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,熟练掌握矩形和折叠的性质,证明三角形相似和三角形全等是解决问题的关键.
【考点精析】关于本题考查的角平分线的性质定理和矩形的性质,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出了甲、乙两种市内移动通讯业务。甲种使用者需每月缴纳15元月租费,然后每通话1分钟,再付花费0.3元;乙种使用者不缴纳月租费,每通话1分钟,付花费0.6元。根据一个月的通话时间,选择哪种方式更优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某文具商场中,每个画板定价为20元,每盒水彩笔定价为5元.为促进销售,商场制定两种优惠方案:一种是买一个画板赠送一盒水彩笔;另一种是按总价九折付款。王老师准备为学校美术小组购买画板4个,水彩笔若干盒(不少于4盒)。
(1)分别求出每种方案下王老师应支付多少元?(用代数式表示)
(2)如果购买24盒水彩笔,哪种方案更省钱?若买50盒水彩笔呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线y=x2﹣x上,且﹣2≤h<1时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.
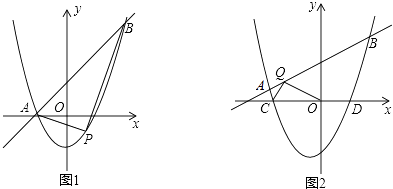
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地居民生活用电基本价格为每度电0.4元,若每月用电量不超过
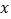 度时,按基本价格收费;若超过
度时,按基本价格收费;若超过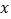 度,超出部分按基本价格的150%收费.
度,超出部分按基本价格的150%收费.(1)某户8月份用电84度,共交电费38.4元,求
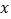 的值。
的值。(2)如果该户9月份的电费平均为每度0.5元,那么该用户9月份用电多少度?应交电费多少元?
相关试题

