【题目】如图，图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（ ） 
A.甲＜乙＜丙
B.乙＜丙＜甲
C.丙＜乙＜甲
D.甲=乙=丙
【答案】D
【解析】解：图1中，甲走的路线长是AC+BC的长度； 延长AD和BF交于C，如图2，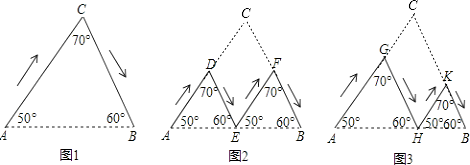
∵∠DEA=∠B=60°，
∴DE∥CF，
同理EF∥CD，
∴四边形CDEF是平行四边形，
∴EF=CD，DE=CF，
即乙走的路线长是AD+DE+EF+FB=AD+CD+CF+BC=AC+BC的长；
延长AG和BK交于C，如图3，
与以上证明过程类似GH=CK，CG=HK，
即丙走的路线长是AG+GH+HK+KB=AG+CG+CK+BK=AC+BC的长；
即甲=乙=丙，
故选D．
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点，需要掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，点
是等边
内一点， 
．将
绕点
按顺时针方向旋转
得
，连接
．
(1)求证： 
是等边三角形；
(2)当
时，试判断
的形状，并说明理由；
(3)探究：当
为多少度时， 
是等腰三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干（它们除颜色外都相同），现随机从中摸出10枚记下颜色后放回，这样连续做了10次，记录了如下的数据：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据，估算袋中的白棋子数量为（ ）
A.60枚
B.50枚
C.40枚
D.30枚
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，已知△ABC 中，其中 A（0，﹣2），B（2，﹣4），C（4，﹣1）．
（1）画出与△ABC 关于 y 轴对称的图形△A1B1C1；
（2）写出△A1B1C1 各顶点坐标；
（3）求△ABC 的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=6cm，AD=4cm，点M是边AB的中点，点P是矩形边上的一个动点，点P从M出发在矩形的边上沿着逆时针方向运动，则当点P沿着矩形的边逆时针旋转一周时，△DMP面积刚好为5cm2的时刻有（ ） 
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是某同学对多项式(a2－4a＋2)(a2－4a＋6)＋4进行因式分解的过程：
解：设a2－4a＝y，则
原式＝(y＋2)(y＋6)＋4(第一步)
＝y2＋8y＋16(第二步)
＝(y＋4)2(第三步)
＝(a2－4a＋4)2.(第四步)
(1)该同学因式分解的结果是否彻底：________(填“彻底”或“不彻底”)；
(2)若不彻底，请你直接写出因式分解的最后结果：________；
(3)请你模仿以上方法对多项式(x2－2x)(x2－2x＋2)＋1进行因式分解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，点O到△ABC的两边AB、AC所在直线的距离相等，且OB=OC．
（1）如图1，若点O在BC上，求证：△ABC是等腰三角形．
（2）如图2，若点O在△ABC内部，求证：AB=AC．
（3）若点O点在△ABC的外部，△ABC是等腰三角形还成立吗？请画图表示．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
