【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)k=8;(2)15;(3) P坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
【解析】
本题考查的是反比例函数的应用
(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义,![]() ,
,![]() ;
;
(3)根据k的几何意义,![]() ,
,![]() .
.
(1)![]() 点
点![]() 横坐标为
横坐标为![]() ,
,![]() 当
当![]() 时,
时,![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 是直线
是直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() .
.
(2)解法一:如图
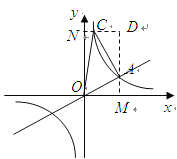
![]() 点
点![]() 在双曲线上,当
在双曲线上,当![]() 时,
时,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
过点![]() 分别做
分别做![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,得矩形
,得矩形![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() .
.
解法二:如图
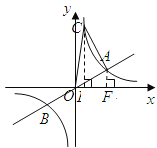
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线
在双曲线![]() 上,当
上,当![]() 时,
时,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.![]() 点
点![]() ,
,![]() 都在双曲线
都在双曲线![]() 上,
上,
![]()
![]() .
.
![]() .
.![]() ,
,![]() .
.
(3)![]() 反比例函数图象是关于原点
反比例函数图象是关于原点![]() 的中心对称图形,
的中心对称图形,
![]() ,
,![]() .
.![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() .
.
设点![]() 横坐标为
横坐标为![]() ,得
,得![]() .
.
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线上,
在双曲线上,![]() .
.
若![]() ,如图
,如图
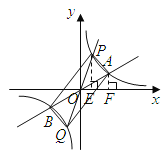
![]() ,
,
![]() .
.![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).![]()
![]() .
.
若![]() ,如图
,如图
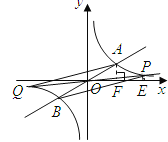
![]() ,
,
![]() .
.![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).![]() .
.
![]() 点
点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第一中学组织七年级部分学生和老师到苏州乐园开展社会实践活动,租用的客车有50座和30座两种可供选择.学校根据参加活动的师生人数计算可知:若只租用30座客车x辆,还差5人才能坐满;
(1)则该校参加此次活动的师生人数为 (用含x的代数式表示);
(2)若只租用50座客车,比只租用30座客车少用2辆,求参加此次活动的师生至少有多少人?
(3)已知租用一辆30座客车往返费用为400元,租用一辆50座客车往返费用为600元,学校根据师生人数选择了费用最低的租车方案,总费用为2200元,试求参加此次活动的师生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )

A.甲<乙<丙
B.乙<丙<甲
C.丙<乙<甲
D.甲=乙=丙 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数的图象与反比例函数的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足分别Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.
(1)求正比例函数解析式、反比例函数解析式.
(2)当点D的纵坐标为9时,求:点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1,并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2,且A2(a,2),C2(-2,b),求a+b的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
相关试题

