【题目】解不等式组 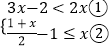 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 . ![]()
参考答案:
【答案】x<2;x≥﹣1; ;﹣1≤x<2
;﹣1≤x<2
【解析】解:解不等式①,得:x<2,
解不等式②,得:x≥﹣1,
把不等式①和②的解集表示在数轴上如下:

故不等式组的解集为:﹣1≤x<2,
所以答案是:(Ⅰ)x<2;(Ⅱ)x≥﹣1;(Ⅳ)﹣1≤x<2.
【考点精析】本题主要考查了不等式的解集在数轴上的表示和一元一次不等式组的解法的相关知识点,需要掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 为线段
为线段 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点 重合,直角边
重合,直角边 、
、 在线段
在线段 上,
上, .
.
(1)将图1中的三角板
 绕着点
绕着点 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若 ,则
,则 ________;猜想
________;猜想 与
与 的数量关系为________;
的数量关系为________;(2)将图1中的三角板
 绕着点
绕着点 沿逆时针方向按每秒
沿逆时针方向按每秒 的速度旋转一周,三角板
的速度旋转一周,三角板 不动,请问几秒时
不动,请问几秒时 所在的直线平分
所在的直线平分 ?
?(3)将图1中的三角板
 绕着点
绕着点 沿逆时针方向按每秒
沿逆时针方向按每秒 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板 绕着点
绕着点 沿顺时针方向按每秒
沿顺时针方向按每秒 的速度旋转(随三角板
的速度旋转(随三角板 停止而停止),请计算几秒时
停止而停止),请计算几秒时 与
与 的角分线共线.
的角分线共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
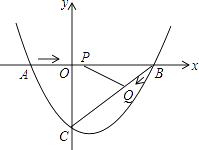
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
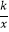 的图象经过点M(2,1)
的图象经过点M(2,1)
(1)求该函数的表达式;
(2)当2<x<4时,求y的取值范围(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响. 试问:

(1)A城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
相关试题

