【题目】如图1,点![]() 为线段
为线段![]() 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点![]() 重合,直角边
重合,直角边![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .
.

(1)将图1中的三角板![]() 绕着点
绕着点![]() 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若![]() ,则
,则![]() ________;猜想
________;猜想![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,三角板
的速度旋转一周,三角板![]() 不动,请问几秒时
不动,请问几秒时![]() 所在的直线平分
所在的直线平分![]() ?
?
(3)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板![]() 绕着点
绕着点![]() 沿顺时针方向按每秒
沿顺时针方向按每秒![]() 的速度旋转(随三角板
的速度旋转(随三角板![]() 停止而停止),请计算几秒时
停止而停止),请计算几秒时![]() 与
与![]() 的角分线共线.
的角分线共线.
参考答案:
【答案】(1)145°,180°;(2)3秒或15秒后OD所在的直线平分∠AOB;(3)![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.
【解析】
(1)根据互余关系先求出∠AOD,再由角的和差求出结果;
(2)当沿逆时针方向旋转45°或225°时,OD所在的直线平分∠AOB,由此便可求得结果;
(3)①当∠COD和∠AOB角平分线夹角为180时,②当∠COD和∠AOB角平分线重合时,即夹角为0°,③当∠COD和∠AOB角平分线重合后再次夹角为180°时,列出关于t的方程进行解答.
解:(1)∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠COD-∠AOC=55°,
∵∠AOB=90°,
∴∠BOD=∠AOB+AOD=145°,
∵∠BOD=∠AOD+∠AOC+BOC,
∴∠AOC+∠BOD=∠AOC+∠AOD+∠AOC+∠BOC=∠COD+∠AOB=90°+90°=180°,
∴∠AOC+∠BOD=∠=180°,
故答案为:145°,180°;
(2)根据题意可得,
当旋转45°或225°时,OD所在的直线平分∠AOB,
所以,旋转时间为:45°÷15°=3(秒),225°÷15°=15(秒),
则3秒或15秒后OD所在的直线平分∠AOB;
(3)起始位置∠COD和∠AOB角平分线夹角为90°,
①当∠COD和∠AOB角平分线夹角为180时,
![]() ,
,
解得![]() (秒);
(秒);
②当∠COD和∠AOB角平分线重合时,即夹角为0°,
![]() ,
,
解得:![]() (秒);
(秒);
③当∠COD和∠AOB角平分线重合后再次夹角为180°时,
![]() ,
,
解得:![]() (秒);
(秒);
综上,![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市组织学术研讨会,需租用客车接送参会人员往返宾馆和观摩地点,客车租赁公司现有
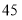 座和
座和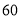 座两种型号的客车可供租用.
座两种型号的客车可供租用.(1)已知
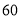 座的客车每辆每天的租金比
座的客车每辆每天的租金比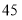 座的贵
座的贵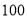 元,会务组第一天在这家公司租了
元,会务组第一天在这家公司租了 辆
辆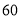 座和
座和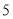 辆
辆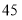 座的客车.一天的租金为
座的客车.一天的租金为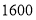 元,求
元,求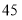 座和
座和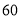 座的客车每辆每天的租金各是多少元?
座的客车每辆每天的租金各是多少元?(2)由于第二天参会人员发生了变化,因此会务纽需重新确定租车方案.
方案1:若只租用
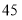 座的客车,会有一辆客车空出
座的客车,会有一辆客车空出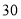 个座位;
个座位;方案2:若只租用
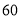 座客车,正好坐满且比只租用
座客车,正好坐满且比只租用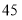 座的客车少用两辆.
座的客车少用两辆.①请计算方案1、2的费用;
②从经济角度考虑,还有方案3吗?如果你是会务纽负责人,应如何确定最终租车方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
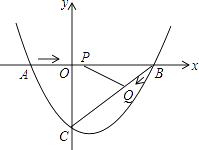
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
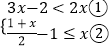 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 .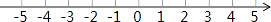
相关试题

