搜索
【题目】已知，如图△ABC中，AB＝5，AC＝3，则中线AD的取值范围是（ ）
A. 2＜AD＜8B. 2＜AD＜4C. 1＜AD＜4D. 1＜AD＜8
参考答案：
【答案】C
【解析】
先延长AD到E，且AD=DE，并连接BE，由于∠ADC=∠BDE，AD=DE，利用SAS易证△ADC≌△EDB，从而可得AC=BE，在△ABE中，再利用三角形三边的关系，可得2<AE<8，从而易求1<AD<4．
延长AD到E，使AD=DE，连接BE，
∵AD=DE,∠ADC=∠BDE,BD=DC，
∴△ADC≌△EDB(SAS)
∴BE=AC=3，
在△AEB中，ABBE<AE<AB+BE，
即53<2AD<5+3，
∴1<AD<4，
∴AD的取值范围是1<AD<4，
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两个一元二次方程：M：ax2+bx+c=0，N：cx2+bx+a=0，其中a+c=0，以下列四个结论中正确的是_____（填写序号）．
①如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根；
②如果方程M有两根符号相同，那么方程N的两根符号也相同；
③如果方程M和方程N有一个相同的根，那么这个根必是x=1；
④如果5是方程M的一个根，那么
是方程N的一个根． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．
（1）求证：四边形ACDF是平行四边形；
（2）当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．分析甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分钟）变化的函数图象，解决下列问题：
（1）求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式；
（2）甲行驶10分钟后，甲、乙两人相距多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】小刚准备用一段长 44 米的篱笆围成三角形，用于养鸡。已知一条边长 x 米，第二条边是第一条边的 3 倍多 6 米。
（1）若能围成一个等腰三角形，求三边长
（2）若第一边长最短，写出 x 的取值范围 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】结果如此巧合!
下面是小颖对一道题目的解答．
题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．
解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．
根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．
根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．
整理，得x2+7x=12．
所以S△ABC=
ACBC=
（x+3）（x+4）=
（x2+7x+12）=
×（12+12）=12．
小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？
请你帮她完成下面的探索．
已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．
可以一般化吗？
（1）若∠C=90°，求证：△ABC的面积等于mn．
倒过来思考呢？
（2）若ACBC=2mn，求证∠C=90°．
改变一下条件……
（3）若∠C=60°，用m、n表示△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,△ABC中，A、B两个顶点在
轴的上方,点C的坐标是(1，0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a，则点B的横坐标是( )
A.
B. 
C. 
D.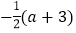 
相关试题
