Question

【题目】如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作EF⊥AB于点F，交AC的延长线于点E．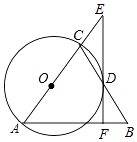
（1）判断EF与⊙O的位置关系，并说明理由；
（2）若AF=6，sinE= ，求BF的长．

Answer 1

【答案】
（1）解：EF与⊙O相切，理由是：

连接OD、AD，

∵AC是⊙O的直径，

∴∠ADC=90°，

∵AB=AC，

∴BD=DC，

∵OA=OC，

∴OD为△ABC的中位线，

∴OD∥AB，

∵EF⊥AB，

∴OD⊥EF，

∴EF与⊙O相切

（2）解：∵OD∥AB，

∴△EOD∽△EAF，

∴ ，

Rt△AEF中，sinE= = ，

∵AF=6，

∴ ，

∴AE=10，

设OD=x，则OA=OD=x，

∴ ，

x= ，

∴OA= ，

∴AC=2OA= ，

∴AB=AC= ，

∴BF=AB﹣AF= ﹣6=

【解析】（1）EF与⊙O相切，先根据等腰三角形三线合一得：BD是高线也是中线，由此得OD是△ABC的中位线，所以OD∥AB，所以OD⊥EF，则EF与⊙O相切；（2）设圆的半径为x，根据△EOD∽△EAF，列比例式求x的值，则直径AC= ，则AB= ，由此可得结论．
【考点精析】利用等腰三角形的性质和直线与圆的三种位置关系对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．