【题目】如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B. 
(1)求该正比例函数的解析式;
(2)将△ABO绕点A逆时针旋转90°得到△ADC,求点C的坐标;
(3)试判断点C是否在直线y= ![]() x+1的图象上,说明你的理由.
x+1的图象上,说明你的理由.
参考答案:
【答案】
(1)解:∵正比例函数y=kx经过点A(2,4),
∴2k=4,解得k=2,
∴该正比例函数的解析式为y=2x
(2)解:∵AB⊥x轴于点B,且A(2,4),
∴OB=2,AB=4.
∵将△ABO绕点A逆时针旋转90°得到△ADC,
∴AD=AB=4,DC=OB=2,
∴D点横坐标为6,C点纵坐标是2,
∴点C的坐标为(6,2)
(3)解:把点C的坐标(6,2)代入y= ![]() x+1,
x+1,
得左边=2,右边= ![]() ×6+1=3,
×6+1=3,
左边≠右边,
即点C不在直线y= ![]() x+1的图象上
x+1的图象上
【解析】(1)将点A(2,4)代入y=kx,利用待定系数法即可求出该正比例函数的解析式;(2)先由AB⊥x轴于点B,且A(2,4),得出OB=2,AB=4.再根据旋转的性质得出AD=AB=4,DC=OB=2,即D点横坐标为6,C点纵坐标是2,进而求出点C的坐标;(3)把点C的坐标(6,2)代入y= ![]() x+1,即可判断.
x+1,即可判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△APB中,AB=2
 ,∠APB=90°,在AB的同侧作正△ABD、正△APE和△BPC,则四边形PCDE面积的最大值是_____.
,∠APB=90°,在AB的同侧作正△ABD、正△APE和△BPC,则四边形PCDE面积的最大值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m
频数
百分数
A级(0≤m<5)
90
0.3
B级(5≤m<10)
120
a
C级(10≤m<15)
b
0.2
D级(m≥15)
30
0.1
请你根据以上信息解答下列问题:

(1)求a,b;
(2)补全频数分布直方图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作EF⊥AB于点F,交AC的延长线于点E.
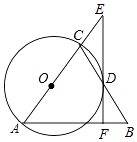
(1)判断EF与⊙O的位置关系,并说明理由;
(2)若AF=6,sinE=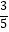 ,求BF的长.
,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=3ax2+2bx+c.
(1)若a=b=1,c=﹣1,求抛物线与x轴公共点的坐标;
(2)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围.
相关试题

