【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)②.
【解析】
(1)欲证明AE=CD,只要证明△ABE≌△CBD;
(2)由△ABE≌△CBD,推出BAE=∠BCD,由∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,又∠CNM=∠ABC,∠ABC=90°,可得∠NMC=90°;
(3)结论:②;作BK⊥AE于K,BJ⊥CD于J.理由角平分线的判定定理证明即可.
(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
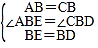 ,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,
又∠CNM=∠ABC,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
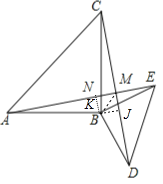
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴![]() AEBK=
AEBK=![]() CDBJ,
CDBJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△ABM≌△DBM,则AB=BD,显然可不能,故①错误.
故答案为②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
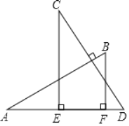
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC=8cm,BC=6cm,D为AB中点,点P在AC上从C向A运动,运动速度为2(cm/s);同时,点Q在BC上从B向C运动,设点Q的运动速度为x(cm/s).且设P,Q的运动时间均为t秒,若其中一点先到达终点,则另一个点也将停止运动.

(1)如图2,当PD∥BC时,请解决下列问题:
①t= ;
②△ADP的形状为 (按“边”分类);
③若此时恰好有△BDQ≌△CPQ,请求出点Q运动速度x的值;
(2)当PD与BC不平行时,也有△BDQ与△CPQ全等:
①请求出相应的t与x的值;
②若设∠A=α°,请直接写出相应的∠DQP的度数(用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根长为6cm的木棍分成两段,每段长分别为a,b(单位:cm)且a,b都为正整数.在直角坐标系中以a,b的值,构成点A(a,b).那么点A落在抛物线y=﹣x2+6x﹣5与x轴所围成的封闭图形内部(如图,不含边界)的概率为 .
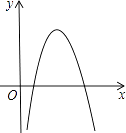
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的顶点A,B的坐标分别是A(﹣1,0),B(0,﹣3),顶点C,D在双曲线y=
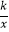 上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= .
上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= . 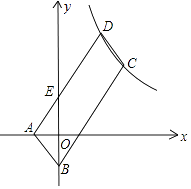
相关试题

