Question

【题目】如图，已知△ABC的三边长为a、b、c，且a＜b＜c，若平行于三角形一边的直线l将△ABC的周长分成相等的两部分．设图中的小三角形①、②、③的面积分别为S1 ， S2 ， S3 ， 则S1 ， S2 ， S3的大小关系是 （用“＜”号连接）

Answer 1

【答案】S1＜S3＜S2
【解析】解：设△ABC的面积为S，周长为C．
①若l∥BC，如图1，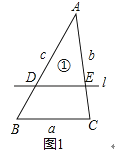

则有△ADE∽△ABC，
∴====；
②若l∥BC，如图2，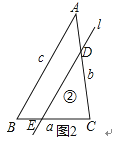

同理可得：=；
③若l∥AC，如图3，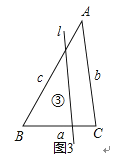

同理可得：= ．
∵0＜a＜b＜c，
∴0＜a+b＜a+c＜b+c，
∴＜＜，
∴S1＜S3＜S2 ，
所以答案是S1＜S3＜S2 ．
设△ABC的面积为S，周长为C．①若l∥BC，如图1，则有△ADE∽△ABC，根据相似三角形的性质及等比性质可得====；②若l∥BC，如图2，同理可得=；③若l∥AC，如图3，同理可得=由0＜a＜b＜c可得0＜a+b＜a+c＜b+c，即可得到＜＜．
【考点精析】通过灵活运用相似三角形的判定与性质，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．