【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
参考答案:
【答案】(1) ;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)24天.
;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)24天.
【解析】
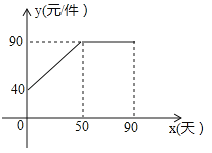
试题分析:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50<x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,套入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当0≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50<x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
试题解析:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b(k、b为常数且k≠0),∵y=kx+b经过点(0,40)、(50,90),∴![]() ,解得:
,解得:![]() ,∴售价y与时间x的函数关系式为y=x+40;
,∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90,∴售价y与时间x的函数关系式为y= .
.
由书记可知每天的销售量p与时间x成一次函数关系,设每天的销售量p与时间x的函数关系式为p=mx+n(m、n为常数,且m≠0),∵p=mx+n过点(60,80)、(30,140),∴![]() ,解得:
,解得:![]() ,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=
,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=![]() ;
;
当50<x≤90时,w=(90﹣30)(﹣2x+200)=﹣120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是 .
.
(2)当0≤x≤50时,w=![]() =
=![]() ,∵a=﹣2<0且0≤x≤50,∴当x=45时,w取最大值,最大值为6050元.
,∵a=﹣2<0且0≤x≤50,∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,w=﹣120x+12000,∵k=﹣120<0,w随x增大而减小,∴当x=50时,w取最大值,最大值为6000元.
∵6050>6000,∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当0≤x≤50时,令w=![]() ≥5600,即
≥5600,即![]() ≥0,解得:30≤x≤50,50﹣30+1=21(天);
≥0,解得:30≤x≤50,50﹣30+1=21(天);
当50<x≤90时,令w=﹣120x+12000≥5600,即﹣120x+6400≥0,解得:50<x≤![]() ,∵x为整数,∴50<x≤53,53﹣50=3(天).
,∵x为整数,∴50<x≤53,53﹣50=3(天).
综上可知:21+3=24(天),故该商品在销售过程中,共有24天每天的销售利润不低于5600元.
-
科目: 来源: 题型:
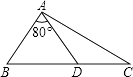
查看答案和解析>>【题目】如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒.
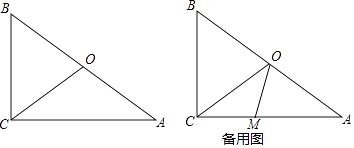
(1)当∠AMO=∠AOM时,求t的值;
(2)当△COM是等腰三角形时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 . -
科目: 来源: 题型:
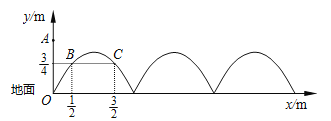
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用
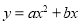 (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为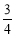 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为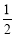 m,
m,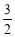 m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需元,购买12根跳绳需元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.求点C到AB的距离.

相关试题

