【题目】如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒. 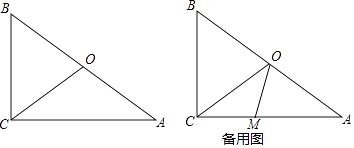
(1)当∠AMO=∠AOM时,求t的值;
(2)当△COM是等腰三角形时,求t的值.
参考答案:
【答案】
(1)解:∵AC=8,BC=6,∠ACB=90°,
∴AB= ![]() =10,
=10,
∵O为AB中点,
∴AO= ![]() AB=5,
AB=5,
∵AO=AM,
∴AM=5,
∴CM=3,
∴t=3;
(2)解:①当CO=CM时,CM=5,
∴t=5
②当MC=MO时,t2=32+(4﹣t)2,
解得:t= ![]() ;
;
③当CO=OM时,M与A点重合,
∴t=8;
综上所述,当△COM是等腰三角形时,t的值为5或 ![]() 或81.
或81.
【解析】(1)由勾股定理求出AB,由直角三角形的性质得出AO=5,求出AM=5,得出CM=3即可;(2)分三种情况讨论,分别求出t的值即可.
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB,根据下列语句画出图形并计算:延长线段AB到C , 使BC=3AB , 反向延长AB到D使AD=
 AB , 取线段DC的中点E , 若AB=4cm,求BE的长.
AB , 取线段DC的中点E , 若AB=4cm,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长和宽分别是
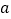 、
、  的矩形纸片的四个角上都剪去一个边长为
的矩形纸片的四个角上都剪去一个边长为 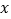 的小正方形,折成一个无盖的纸盒.
的小正方形,折成一个无盖的纸盒.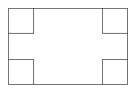
(1)用a , b , x表示纸片剩余部分的面积;
(2)当a=16,b=12,且剪去部分的面积等于剩余部分的面积的一半时,求小正方形的边长. -
科目: 来源: 题型:
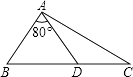
查看答案和解析>>【题目】如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 . -
科目: 来源: 题型:
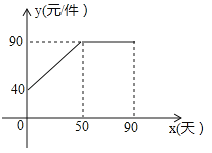
查看答案和解析>>【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
-
科目: 来源: 题型:
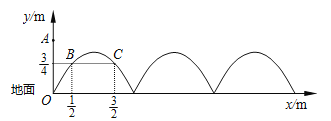
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用
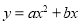 (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为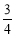 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为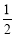 m,
m,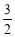 m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
相关试题

