【题目】如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.求点C到AB的距离. 
参考答案:
【答案】解:在AB上截取AE=AC=3,连接CE,过C作CF⊥AB于F点. 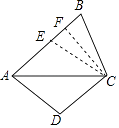
∵AC平分∠BAD,
∴∠BAC=∠DAC.
在△ADC与△AEC中,
∵ 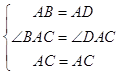 ,
,
∴△ADC≌△AEC(SAS),
∴CE=CD.
∵CD=CB,
∴CE=CB.
∵CF⊥BE,
∴CF垂直平分BE.
∵AB=5,
∴BE=2,
∴EF=1,
∴AF=4,
在Rt△ACF中,
∵CF2=AC2﹣AF2=52﹣42=9,
∴CF=3.
【解析】在AB上截取AE=AC=3,连接CE,过C作CF⊥AB于F点,根据SAS定理得出△ADC≌△AEC,故可得出CE=CD,再由垂直平分线的性质求出AF的长,根据勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
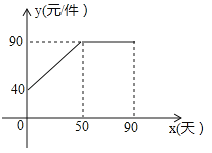
查看答案和解析>>【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
-
科目: 来源: 题型:
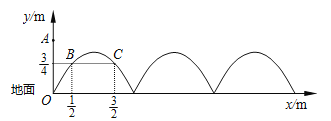
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用
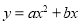 (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为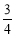 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为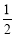 m,
m,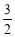 m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需元,购买12根跳绳需元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边分别为3,x,4,那么x的取值范围是_______
-
科目: 来源: 题型:
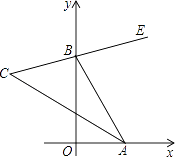
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
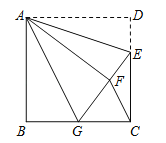
A.2 B.3 C.4 D.5
相关试题

