【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
参考答案:
【答案】
(1)∵∠BOC+∠AOC=180°,∠BOC=120°∴∠AOC=60°。∵OM平分∠BOC,∴∠COM=![]() ∠BOC=
∠BOC=![]()
![]() 120°=60°,∵∠AOM=∠AOC+∠COM,∴∠AOM=60°+60°=120°答案:120
120°=60°,∵∠AOM=∠AOC+∠COM,∴∠AOM=60°+60°=120°答案:120
(2)解:如图3,
∵∠BOC=120°,
∴∠A0C=60°,∠AOM转化成∠MON-∠AON,∠NOC转化成∠AOC-∠AON,
∵∠AON=90°﹣∠AOM=60°﹣∠NOC,
∴∠AOM﹣∠NOC=30°
(3)解:设三角板绕点O旋转的时间是x秒,∵∠BOC=120°,∴∠AOC=60°,当逆时针旋转60°或逆时针旋转240°时 ON平分∠AOC,于是可列10x=60或10x=240,∴x=6或x=24,即此时三角板绕点O旋转的时间是6秒或24秒.故答案为:6秒或24秒
【解析】(1)根据OM恰好平分∠BOC,求出∠COM的度数,再根据∠BOC与∠AOC互为邻补角,求出∠AOC的度数,然后根据∠AOM=∠AOC+∠COM,即可求出结果。
(2)先根据∠BOC与∠AOC互为邻补角,求出∠AOC的度数,再根据已知可知∠MON=90°,∠AON=90°-∠AOM,∠AON=60°-∠NOC,然后建立方程,变形即可得出结论。
(3)根据∠AOC=60°,可知当逆时针旋转60°或逆时针旋转240°时 ON平分∠AOC,设未知数建立方程,求解即可。
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长和宽分别是
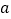 、
、  的矩形纸片的四个角上都剪去一个边长为
的矩形纸片的四个角上都剪去一个边长为 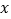 的小正方形,折成一个无盖的纸盒.
的小正方形,折成一个无盖的纸盒.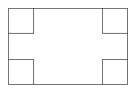
(1)用a , b , x表示纸片剩余部分的面积;
(2)当a=16,b=12,且剪去部分的面积等于剩余部分的面积的一半时,求小正方形的边长. -
科目: 来源: 题型:
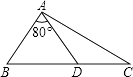
查看答案和解析>>【题目】如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒.
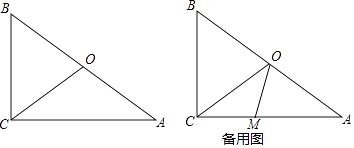
(1)当∠AMO=∠AOM时,求t的值;
(2)当△COM是等腰三角形时,求t的值. -
科目: 来源: 题型:
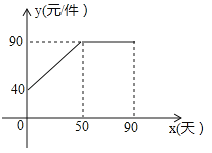
查看答案和解析>>【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
-
科目: 来源: 题型:
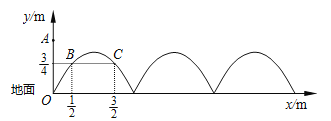
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用
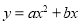 (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为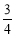 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为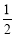 m,
m,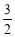 m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需元,购买12根跳绳需元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
相关试题

