【题目】平面内的两条直线有相交和平行两种位置关系.




(1)如图1,若![]() ,点
,点![]() 在
在![]() 外部,则有
外部,则有![]() ,又可证
,又可证![]() ,得
,得![]() ,将点
,将点![]() 移到
移到![]() 内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则
内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则![]() 之间有何数量关系?请证明你的结论;
之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() 如图3,则
如图3,则![]()
![]() 之间有何数量关系? (不需证明);
之间有何数量关系? (不需证明);
(3)根据(2)的结论,求如图4中![]() 的度数.
的度数.
参考答案:
【答案】(1)不成立,![]() ;证明见解析;(2)
;证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)延长BP交CD于点E,根据AB∥CD得出∠B=∠BED,再由三角形外角的性质即可得出结论;
(2)连接QP并延长,由三角形外角的性质得出∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,由此可得出结论;
(3)由(2)的结论得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.再根据∠A+∠AFG+∠AGF=180°即可得出结论.
解:(1)不成立,结论是∠BPD=∠B+∠D.
延长BP交CD于点E,
∵AB∥CD,
∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;

(2)结论:∠BPD=∠BQD+∠B+∠D.
连接QP并延长,
∵∠BPE是△BPQ的外角,∠DPE是△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,
即∠BPD=∠BQD+∠B+∠D;

(3)由(2)的结论得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.
又∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.

(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=
 AB.
AB.灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
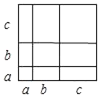
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形 的面积(结果保留根号);
的面积(结果保留根号);
相关试题

