Question

【题目】阅读理解：在以后你的学习中，我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半，即：如图1，在Rt△ABC中，∠ACB＝90°，若点D是斜边AB的中点，则CD＝AB．

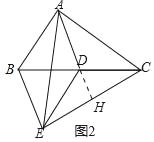
灵活应用：如图2，△ABC中，∠BAC＝90°，AB＝6，AC＝8，点D是BC的中点，连接AD，将△ACD沿AD翻折得到△AED，连接BE，CE．

（1）填空：AD＝　 　；

（2）求证：∠BEC＝90°；

（3）求BE．

Answer 1

【答案】（1）5；（2）证明见解析；（3）.

【解析】

（1）利用勾股定理求出BC，再利用阅读理解中的结论即可解决问题；

（2）由将△ACD沿AD翻折得到△AED，推出CD＝DE＝BD，推出∠DBE＝∠DEB，∠DCE＝∠DEC，由∠DBF+∠DEB+∠DEC+∠DCE＝180°，推出2∠DEB+2∠DEC＝180°，可得∠DEB+∠DEC＝90°；

（3）如图2中，延长AD交EC于H．由△ACB∽△HAC，＝，求出AH，DH，再证明BE＝2DH即可解决问题；

（1）解：在Rt△ABC中，∵∠BAC＝90°，AB＝6，AC＝8，

∴BC＝＝10，

∵BD＝DC，

∴AD＝BC＝5，

故答案为5；

（2）证明：∵将△ACD沿AD翻折得到△AED，

∴CD＝DE＝BD，

∴∠DBE＝∠DEB，∠DCE＝∠DEC，

∵∠DBF+∠DEB+∠DEC+∠DCE＝180°，

∴2∠DEB+2∠DEC＝180°，

∴∠DEB+∠DEC＝90°，

∴∠BEC＝90°；

（3）解：如图2中，延长AD交EC于H．

∵AE＝AE，∠HAE＝∠HAC，

∴AH⊥EC，

∴EH＝CH，

∵BD＝CD，

∴BE＝2DH，

∵DA＝DC，

∴∠ACB＝∠CAH，

∵∠CAB＝∠AHC＝90°，

∴△ACB∽△HAC，

∴＝，

∴＝，

∴AH＝，

∴DH＝AH﹣AD＝﹣5＝，

∴BE＝2DH＝．