【题目】已知,如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
试求:(1)![]() 的度数;(2)四边形
的度数;(2)四边形![]() 的面积(结果保留根号);
的面积(结果保留根号);
参考答案:
【答案】(1)![]() ;
;
(2)![]()
【解析】
(1)连接AC,由勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACD的形状,进而可求出∠BAD的度数;
(2)由(1)可知△ABC和△ADC是Rt△,再根据S四边形ABCD=S△ABC+S△ADC即可得出结论.
解:(1)连接AC,如图所示:
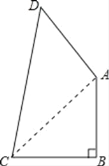
∵AB=BC=1,∠B=90°
∴AC=![]() ,
,
又∵AD=1,DC=![]() ,
,
∴ AD2+AC2=3 CD2=(![]() )2=3
)2=3
即CD2=AD2+AC2
∴∠DAC=90°
∵AB=BC=1
∴∠BAC=∠BCA=45°
∴∠BAD=135°;
(2)由(1)可知△ABC和△ADC是Rt△,
∴S四边形ABCD=S△ABC+S△ADC=1×1×![]() +1×
+1×![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
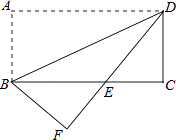
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C在数轴上,O为原点,且BO:OC:CA=2:1:5.
(1)如果点C表示的数是x,请直接写出点A、B表示的数;
(2)如果点A表示的数比点C表示的数两倍还大4,求线段AB的长.
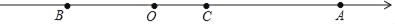
-
科目: 来源: 题型:
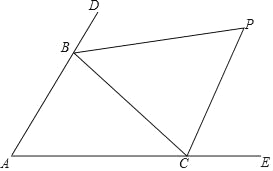
查看答案和解析>>【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小伙李明刚多次将“宜昌柠檬”从宜昌市运往A市销售,市场调查发现:运往A市的火车与汽车的平均速度分别为100千米/时和80千米/时,运输费分别为每千米15m元和20m元,装卸费分别为2000m元和900m元(m为正数),火车、汽车装卸时间为2小时,运输过程中的损耗均为200m元/时.
(1)如果宜昌市与A市之间的路程400千米,求汽车的三费(装卸费、运输费、耗损费)比火车的三费多多少元?
(2)如果宜昌市与A市之间的路程为S千米,火车与汽车在运输途中停误的时间分别是2小时和3.1小时,请你通过计算说明,李明刚选择哪种方式比校合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
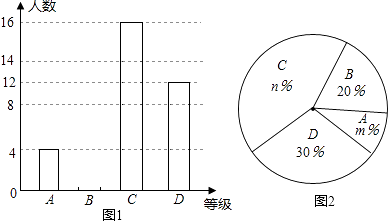
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
相关试题

