【题目】若一个四位自然数满足个位与百位相同,十位与千位相同,我们称这个数为“双子数”.将“双子数”![]() 的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数
的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数![]() ,记
,记![]() 为“双子数”
为“双子数”![]() 的“双11数”.例如,
的“双11数”.例如,![]() ,
,![]() ,则
,则![]() .
.
(1)计算2424的“双11数”![]() ______;
______;
(2)若“双子数”![]() 的“双11数”的
的“双11数”的![]() 是一个完全平方数,求
是一个完全平方数,求![]() 的值;
的值;
(3)已知两个“双子数”![]() 、
、![]() ,其中
,其中![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() 、
、![]() 、
、![]() 、
、![]() 都为整数,若
都为整数,若![]() 的“双11数”
的“双11数”![]() 能被17整除,且
能被17整除,且![]() 、
、![]() 的“双11数”满足
的“双11数”满足![]() ,令
,令![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)12;(2)4或16或36;;(3)51或17.
【解析】
(1)直接根据“双子数”m的“双11数”的计算方法即可得出结论;
(2)设出四位数,进而得出F(m)=2(x+y),再求出0<x+y≤18,再根据F(m)是一个完全平方数,求出x+y,即可得出结论;
(3)先根据“双11数”F(p)能被17整除,进而判断出p为8989,求出F(q)=2(c+d),再根据F(p)+2F(q)﹣(4a+3b+2d+c)=0,得出d![]() ,进而求出c,d,即可得出结论.
,进而求出c,d,即可得出结论.
(1)由题意知,2424的“双11数”F(2424)![]() 12.
12.
故答案为:12;
(2)设“双子数”m的个位数字和十位数字分别为x,y,(0≤x≤9,0<y≤9)
则数字m为1000y+100x+10y+x=1010y+101x,
∴“双子数”m'为1010x+101y,
∴F(m)![]() 2(x+y).
2(x+y).
∵0≤x≤9,0<y≤9,
∴0<x+y≤18.
∵F(m)是一个完全平方数,
∴2(x+y)是一个完全平方数,
∴x+y=2或x+y=8或x+y=18,
∴F(m)=2×2=4或16或36,
即:F(m)的值为4或16或36;
(3)∵“双子数”p,p![]() ,
,
∴F(p)=2(a+b).
∵“双11数”F(p)能被17整除,
∴a+b是17的倍数.
∵1≤a<b≤9,
∴3≤a+b<18,
∴a+b=17,
∴a=8,b=9,
∴“双子数”p为8989,F(p)=34.
∵“双子数”q,q![]() ,
,
∴F(q)=2(c+d).
∵F(p)+2F(q)﹣(4a+3b+2d+c)=0,
∴34+2×2(c+d)﹣(4×8+3×9+2d+c)=0,
∴3c+2d=25,
∴d![]() ,
,
∵1≤c≤9,1≤d≤9,c≠d,c、d都为整数,
∴c为奇数,1≤c<9,
当c=1时,d=11,不符合题意,舍去,
当c=3时,d=8,
∴“双子数”q为3838,
∴G(p,q)![]() 51,
51,
当c=5时,d=5,不符合题意,舍去,
当c=7时,d=2,
∴“双子数”q为7272,
∴G(p,q)![]() 17,
17,
∴G(p,q)的值为51或17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
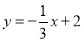 过点
过点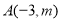 且与
且与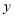 轴交于点
轴交于点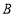 ,点
,点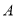 关于
关于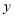 轴的对称点为点
轴的对称点为点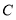 .过点
.过点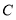 且与直线
且与直线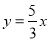 平行的直线交
平行的直线交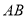 于点
于点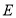 ,交
,交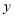 轴于点
轴于点 ,连接
,连接 .
.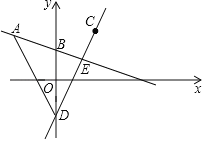
(1)求直线
 的解析式;
的解析式;(2)求
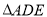 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】据农业农村部消息,国内受猪瘟与猪周期叠加影响,生猪供应量大幅减少,从今年6月起猪肉价格连续上涨一品生鲜超市在6月1日若售出
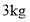 五花肉和
五花肉和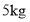 排骨,销售额为366元;若售出
排骨,销售额为366元;若售出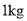 五花肉和
五花肉和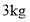 排骨,销售额为186元.
排骨,销售额为186元.(1)6月1日每千克五花肉和排骨的价格各是多少元?
(2)6月1日五花肉和排骨的销售量分别为
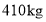 、
、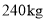 由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了
由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了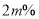 ,销售量减少了
,销售量减少了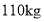 ;排骨的销售价格在6月1日的基础上增加了
;排骨的销售价格在6月1日的基础上增加了 元,销售量下降了
元,销售量下降了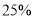 .结果1l月1日的销售额比6月1日的销售额多5100元,求
.结果1l月1日的销售额比6月1日的销售额多5100元,求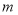 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数关系式;
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
-
科目: 来源: 题型:
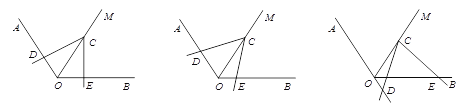
查看答案和解析>>【题目】如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线
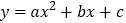 (a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣
(a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣ ),该抛物线与BE交于另一点F,连接BC.
),该抛物线与BE交于另一点F,连接BC.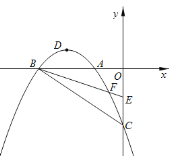
(1)求该抛物线的解析式,并用配方法把解析式化为
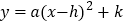 的形式;
的形式;(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,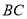 的垂直平分线
的垂直平分线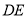 交
交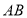 于点
于点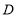 ,交
,交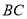 于点
于点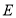 .
.(1)如图1,若
 ,
,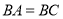 ,
,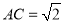 ,求
,求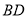 的长;
的长;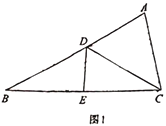
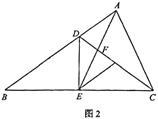
(2)如图2,连接
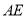 交
交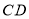 于点
于点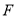 ,若
,若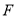 为
为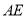 的中点,且满足
的中点,且满足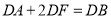 ,求证:
,求证: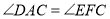 .
.
相关试题

