【题目】在![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
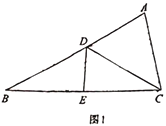
(1)如图1,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
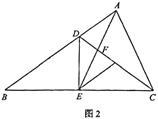
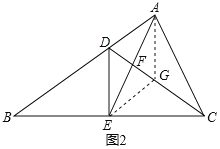
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点,且满足
的中点,且满足![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)作AF⊥CD于F,由线段垂直平分线的性质得出BD=CD,由等腰三角形的性质得出∠DCB=∠B=30°,∠BAC=∠BCA=75°,求出∠ACF=45°,得出△ACF是等腰直角三角形,得出AF=1,∠FAC=45°,由直角三角形的性质得出DF的长,即可得出答案;
(2)作AG∥DE交CD于G,则∠GAF=∠DEF,证明△AFG≌△EFD(ASA),得出AG=ED,GF=DF,证出四边形ADEG是平行四边形,得出AD=EG,∠DAG+∠ADE=180°,证明△ADE≌△CGA(SAS),得出∠DAE=∠GCA,进而得出结论.
(1)作AF⊥CD于F,如图1所示:
∵DE是BC的垂直平分线,
∴BD=CD,
∴∠DCB=∠B=30°.
∵BA=BC,
∴∠BAC=∠BCA![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠ACF=75°﹣30°=45°.
∵AF⊥CD,
∴△ACF是等腰直角三角形,
∴AF=CF![]() AC=1,∠FAC=45°,
AC=1,∠FAC=45°,
∴∠DAF=30°,
∴DF![]() AF
AF![]() ,
,
∴BD=CD=CF+DF=![]() ;
;
(2)作AG∥DE交CD于G,如图2所示:
则∠GAF=∠DEF.
∵F为AE的中点,
∴AF=EF.
在△AFG和△EFD中,
∵ ,
,
∴△AFG≌△EFD(ASA),
∴AG=ED,GF=DF.
∵AG∥ED,
∴四边形ADEG是平行四边形,
∴AD=EG,∠DAG+∠ADE=180°.
∵DA+2DF=DB=DC,DC=DF+GF+CG,
∴AD=CG=EG,
∴∠GEC=∠GCE.
∵∠GEC+∠DEG=∠GCE+∠GDE=90°,
∴∠DEG=∠GDE,
∴DG=EG=CG=AD,
∴∠DAG=∠DGA.
∵∠DGA+∠CGA=180°,
∴∠ADE=∠CGA.
在△ADE和△CGA中,
∵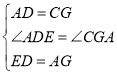 ,
,
∴△ADE≌△CGA(SAS),
∴∠DAE=∠GCA.
∵∠DAC=∠DAE+∠CAF,∠EFC=∠GCA+∠CAF,
∴∠DAC=∠EFC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四位自然数满足个位与百位相同,十位与千位相同,我们称这个数为“双子数”.将“双子数”
 的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数
的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数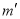 ,记
,记 为“双子数”
为“双子数” 的“双11数”.例如,
的“双11数”.例如,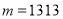 ,
,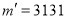 ,则
,则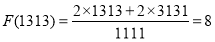 .
.(1)计算2424的“双11数”
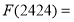 ______;
______;(2)若“双子数”
 的“双11数”的
的“双11数”的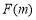 是一个完全平方数,求
是一个完全平方数,求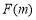 的值;
的值;(3)已知两个“双子数”
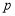 、
、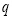 ,其中
,其中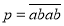 ,
,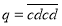 (其中
(其中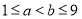 ,
,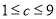 ,
,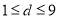 ,
,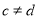 且
且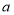 、
、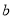 、
、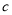 、
、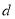 都为整数,若
都为整数,若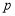 的“双11数”
的“双11数”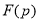 能被17整除,且
能被17整除,且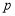 、
、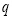 的“双11数”满足
的“双11数”满足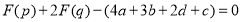 ,令
,令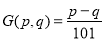 ,求
,求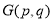 的值.
的值. -
科目: 来源: 题型:
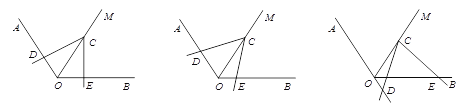
查看答案和解析>>【题目】如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线
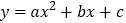 (a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣
(a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣ ),该抛物线与BE交于另一点F,连接BC.
),该抛物线与BE交于另一点F,连接BC.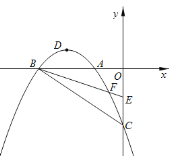
(1)求该抛物线的解析式,并用配方法把解析式化为
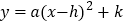 的形式;
的形式;(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
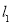 :
: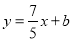 与直线
与直线 :
: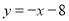 交于点
交于点 ,已知点
,已知点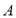 的横坐标为-5,直线
的横坐标为-5,直线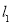 与
与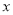 轴交于点
轴交于点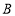 ,与
,与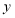 轴交于点
轴交于点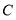 ,直线
,直线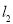 与
与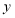 轴交于点
轴交于点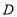 .
.
(1)求直线
 的解析式;
的解析式;(2)将直线
 向上平移6个单位得到直线
向上平移6个单位得到直线 ,直线
,直线 与
与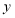 轴交于点
轴交于点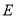 ,过点
,过点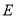 作
作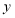 轴的垂线
轴的垂线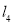 ,若点
,若点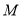 为垂线
为垂线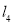 上的一个动点,点
上的一个动点,点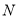 为
为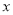 轴上的一个动点,当
轴上的一个动点,当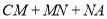 的值最小时,求此时点
的值最小时,求此时点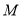 的坐标及
的坐标及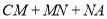 的最小值;
的最小值;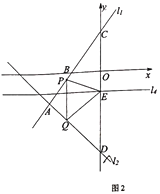
(3)已知点
 、
、 分别是直线
分别是直线 、
、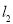 上的两个动点,连接
上的两个动点,连接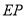 、
、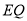 、
、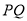 ,是否存在点
,是否存在点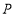 、
、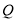 ,使得
,使得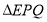 是以点
是以点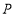 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.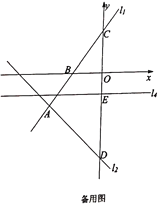
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线
 经过点
经过点 ,直线
,直线 经过点
经过点 ,且
,且 与
与 关于
关于 轴对称,则
轴对称,则 与
与 的交点坐标为( )
的交点坐标为( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2+(2k﹣1)x+k2=0的两根a、b满足a2﹣b2=0,双曲线
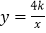 (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )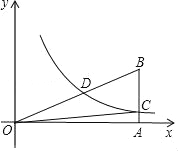
A. 3 B.
 C. 6 D. 3或
C. 6 D. 3或
相关试题

