【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .过点
.过点![]() 且与直线
且与直线![]() 平行的直线交
平行的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
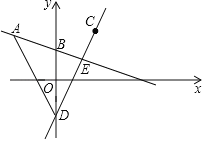
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)10.
;(2)10.
【解析】
(1)先求得A的坐标,即可求得C的坐标,根据题意设直线CD的解析式为y![]() x+b,代入C的坐标,根据待定系数法求得即可;
x+b,代入C的坐标,根据待定系数法求得即可;
(2)根据图象坐标特征求得B、D的坐标,然后解析式联立求得E的坐标,根据S△ADE=S△ABD+S△EBD即可求得.
(1)∵直线y![]() x+2过点A(﹣3,m),
x+2过点A(﹣3,m),
∴m![]() (﹣3)+2=3,
(﹣3)+2=3,
∴A(﹣3,3).
∵点A关于y轴的对称点为点C,
∴C(3,3).
∵直线CD与直线y![]() x平行,
x平行,
∴设直线CD的解析式为y![]() x+b,
x+b,
代入C(3,3)得:3![]() 3+b,
3+b,
解得:b=﹣2,
∴直线CD的解析式为![]() ;
;
(2)在直线y![]() x+2中,令x=0,则y=2,
x+2中,令x=0,则y=2,
∴B(0,2),
在直线y![]() x﹣2中,令x=0,则y=﹣2,
x﹣2中,令x=0,则y=﹣2,
∴D(0,﹣2),
∴BD=4,
解 ,得
,得![]() ,
,
∴E(2,![]() ),
),
∴S△ADE=S△ABD+S△EBD![]() 10.
10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】活跃校园气氛,增强班集体凝聚力,培养学生团结协作意识,重庆一中举行了秋季趣味运动会.赛后为了了解初二年级的学生们对新增比赛项目“毛毛虫赛跑”的喜欢程度(以下称:喜欢度),对该年级的学生进行了调查,被调查的学生对该比赛项目的喜欢度分别记为:5分、4分、3分、2分、1分(其中5分为超喜欢、4分为很喜欢、3分为喜欢、2分为一般、1分为不喜欢),并将调查结果绘制成如下两幅不完整的统计图:
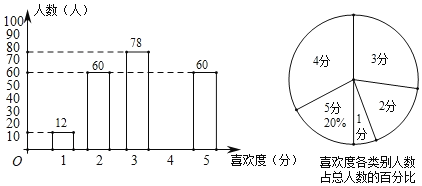
请你根据图中提供的信息,回答下列问题:
(1)被调查的学生总数是______人,并补全条形统计图;
(2)写出被调查学生喜欢度分数的中位数是______分,众数是______分;
(3)求这批被调查学生喜欢度分数的平均数.
-
科目: 来源: 题型:
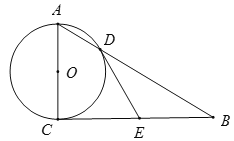
查看答案和解析>>【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究函数
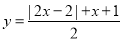 的图象和性质.洋洋同学根据学习函数的经验,对函数
的图象和性质.洋洋同学根据学习函数的经验,对函数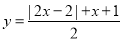 的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成: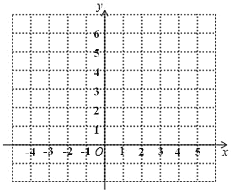
(1)化简函数解析式:当
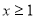 时,
时,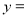 ______,当
______,当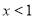 时,
时,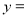 ______;
______;(2)根据(1)的结果,请在所给坐标系中画出函数
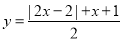 的图象;(直尺画图,不用列表)
的图象;(直尺画图,不用列表)(3)观察函数图象,请写出该函数的一条性质:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据农业农村部消息,国内受猪瘟与猪周期叠加影响,生猪供应量大幅减少,从今年6月起猪肉价格连续上涨一品生鲜超市在6月1日若售出
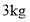 五花肉和
五花肉和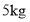 排骨,销售额为366元;若售出
排骨,销售额为366元;若售出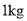 五花肉和
五花肉和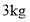 排骨,销售额为186元.
排骨,销售额为186元.(1)6月1日每千克五花肉和排骨的价格各是多少元?
(2)6月1日五花肉和排骨的销售量分别为
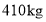 、
、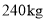 由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了
由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了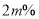 ,销售量减少了
,销售量减少了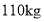 ;排骨的销售价格在6月1日的基础上增加了
;排骨的销售价格在6月1日的基础上增加了 元,销售量下降了
元,销售量下降了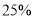 .结果1l月1日的销售额比6月1日的销售额多5100元,求
.结果1l月1日的销售额比6月1日的销售额多5100元,求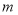 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数关系式;
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四位自然数满足个位与百位相同,十位与千位相同,我们称这个数为“双子数”.将“双子数”
 的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数
的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数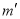 ,记
,记 为“双子数”
为“双子数” 的“双11数”.例如,
的“双11数”.例如,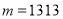 ,
,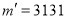 ,则
,则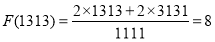 .
.(1)计算2424的“双11数”
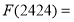 ______;
______;(2)若“双子数”
 的“双11数”的
的“双11数”的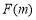 是一个完全平方数,求
是一个完全平方数,求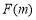 的值;
的值;(3)已知两个“双子数”
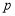 、
、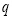 ,其中
,其中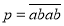 ,
,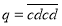 (其中
(其中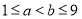 ,
,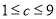 ,
,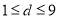 ,
,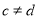 且
且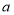 、
、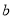 、
、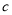 、
、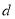 都为整数,若
都为整数,若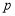 的“双11数”
的“双11数”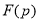 能被17整除,且
能被17整除,且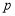 、
、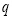 的“双11数”满足
的“双11数”满足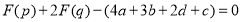 ,令
,令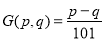 ,求
,求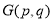 的值.
的值.
相关试题

