【题目】如图,已知E为等腰△ABC的底边BC上一动点,过E作EF⊥BC交AB于D,交CA的延长线于F,问: 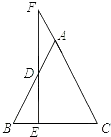
(1)∠F与∠ADF的关系怎样?说明理由;
(2)若E在BC延长线上,其余条件不变,上题的结论是否成立?若不成立,说明理由;若成立,画出图形并给予证明.
参考答案:
【答案】
(1)解:∠F=∠ADF
理由:∵AB=AC
∴∠B=∠C
∵EF⊥BC
∴∠B+∠BDE=90°,∠C+∠F=90°
∴∠BDE=∠F
∵∠ADF=∠BDE
∴∠ADF=∠F
(2)解:成立
证明:∵AB=AC
∴∠B=∠ACB
∵∠ACB=∠ECF
∴∠B=∠ECF
∵EF⊥BC
∴∠B+∠BDE=90°,∠ECF+∠F=90°
∴∠BDE=∠F
即∠ADF=∠F.
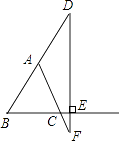
【解析】由已知条件,根据等腰三角形两底角相等及三角形两锐角互余的性质不难推出∠F与∠ADF的关系.
-
科目: 来源: 题型:
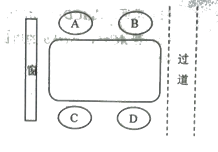
查看答案和解析>>【题目】莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
(1)请用适当的方法表示出所有的不同就座方案.
(2)请问隆迪恰好坐在靠近过道一侧的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?
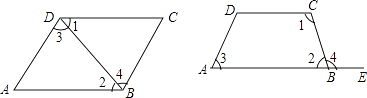
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
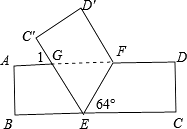
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A.三点确定一个圆
B.平分弦的直径垂直于弦
C.圆有无数条对称轴,任何一条直径都是它的对称轴
D.同弧或等弧所对圆心角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长的关系是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明:
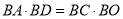 ;
;(3)若AC=5,BC=12,求⊙O的半径.
相关试题

