【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.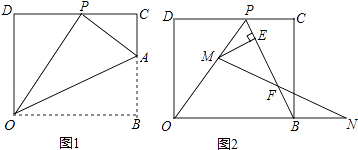
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可
参考答案:
【答案】
(1)
解:∵D(0,8),
∴OD=BC=8,
∵OD=2CP,
∴CP=4,
设OB=OP=DC=x,
则DP=x﹣4,
在Rt△ODP中,OD2+DP2=OP2,
即:82+(x﹣4)2=x2,
解得:x=10,
∵∠OPA=∠B=90°,
∴△ODP∽△PCA,
∴OD:PC=DP:CA,
∴8:4=(x﹣4):AC,
则AC= ![]() =3,
=3,
∴AB=5,
∴点A(10,5);
(2)
解:∵点 P 恰好是CD边的中点,
设DP=PC=y,
则DC=OB=OP=2y,
在Rt△ODP中,OD2+DP2=OP2,
即:82+y2=(2y)2,
解得:y= ![]() ,
,
∵∠OPA=∠B=90°,
∴△ODP∽△PCA,
∴OD:PC=DP:CA,
∴8:y=y:AC,
则AC= ![]() =
= ![]() ,
,
∴AB=8﹣ ![]() =
= ![]() ,
,
∵OB=2y= ![]() ,
,
∴tan∠AOB= ![]() =
= ![]() =
= ![]() ,
,
∴∠AOB=30°;
(3)
解:作MQ∥AN,交PB于点Q,如图2,
∵AP=AB,MQ∥AN
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ= ![]() PQ.
PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
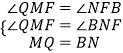 ,
,
∴△MFQ≌△NFB(AAS).
∴QF= ![]() QB,
QB,
∴EF=EQ+QF= ![]() PQ+
PQ+ ![]() QB=
QB= ![]() PB,
PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB= ![]() =4
=4 ![]() ,
,
∴EF= ![]() PB=2
PB=2 ![]() ,
,
∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为2 ![]() .
.

【解析】(1)设OB=OP=DC=x,则DP=x﹣4,在Rt△ODP中,根据OD2+DP2=OP2 , 解得:x=10,然后根据△ODP∽△PCA得到AC= ![]() =3,从而得到AB=5,表示出点A(10,5);(2)根据点P恰好是CD边的中点设DP=PC=y,则DC=OB=OP=2y,在Rt△ODP中,根据OD2+DP2=OP2 , 解得:y=
=3,从而得到AB=5,表示出点A(10,5);(2)根据点P恰好是CD边的中点设DP=PC=y,则DC=OB=OP=2y,在Rt△ODP中,根据OD2+DP2=OP2 , 解得:y= ![]() ,然后利用△ODP∽△PCA得到AC=
,然后利用△ODP∽△PCA得到AC= ![]() =
= ![]() ,从而利用tan∠AOB=
,从而利用tan∠AOB= ![]() 得到∠AOB=30°;(3)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=
得到∠AOB=30°;(3)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ= ![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF= ![]() QB,再求出EF=
QB,再求出EF= ![]() PB,由(1)中的结论求出PB,最后代入EF=
PB,由(1)中的结论求出PB,最后代入EF= ![]() PB即可得出线段EF的长度不变.
PB即可得出线段EF的长度不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△
 中,
中,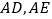 分别是△
分别是△ 的高和角平分线,若
的高和角平分线,若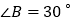 ,
,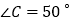 ;求
;求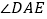 的度数.
的度数.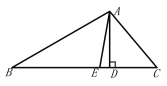
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.

(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1 , 四边形DECB的面积为S2 , 求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.

(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
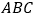 中,
中,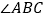 的平分线与
的平分线与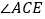 的平分线相交于点
的平分线相交于点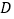 .
.⑴.若
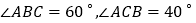 ,求
,求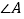 和
和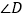 度数;
度数;⑵.由第⑴小题的计算,发现
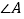 和
和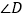 有什么关系?它们是不是一定有这种关系?请作出说明.
有什么关系?它们是不是一定有这种关系?请作出说明.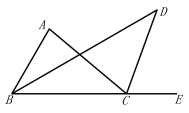
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
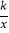 (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )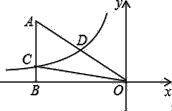
A. 6 B. 12 C. 18 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的边心距为
 ,这个正六边形的面积为( )
,这个正六边形的面积为( )
A.2
B.4
C.6
D.12
相关试题

