【题目】某厂家新开发的一种摩托车如图所示，它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°，大灯A离地面距离1m．

（1）该车大灯照亮地面的宽度BC约是多少（不考虑其它因素）？

（2）一般正常人从发现危险到做出刹车动作的反应时间是0.2s，从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离，某人以60km/h的速度驾驶该车，从60km/h到摩托车停止的刹车距离是m，请判断该车大灯的设计是否能满足最小安全距离的要求，请说明理由．（参考数据： ，， ， ）

参考答案：

【答案】该车大灯照亮地面的宽度BC是1.4m；

（2）该车大灯的设计不能满足最小安全距离的要求．理由见解析.

【解析】（1）通过构造直角三角形来解答，过A作AD⊥MN于D，就有了∠ABN、∠ACN的度数，又已知AE的长，可在直角三角形ABE、ACE中分别求出BE、CE的长，BC就能求出（2）时间由60km/h小时转化为m∕s，再由速度×时间=路程，即可求解.

本题解析：如图

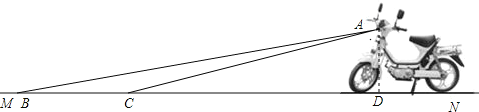
（1）过A作AD⊥MN于点D，

在Rt△ACD中, tan∠ACD= =, CD=5.6(m)，

在Rt△ABD中,

tan∠ABD= =, BD=7(m)，

则BC=75.6=1.4(m).

答：该车大灯照亮地面的宽度BC是1.4m.

（2）该车大灯的设计不能满足最小安全距离的要求．

理由如下：∵以60 km/h的速度驾驶，

∴速度还可以化为： m/s，

最小安全距离为： ×0.2+ =8（m），

大灯能照到的最远距离是BD=7m，

∴该车大灯的设计不能满足最小安全距离的要求．

关闭