【题目】(6分)如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).

(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
参考答案:
【答案】(1)y=![]() ,B(2,4);(2)x>2或-4<x<0.
,B(2,4);(2)x>2或-4<x<0.
【解析】试题分析:(1)设反比例函数的解析式为y=(k≠0),把A点坐标代入即可得出k的值,进而得出反比例函数的解析式,再把B点坐标代入即可得出a的值,利用待定系数法即可得出一次函数的解析式;
(2)直接根据两函数的交点即可得出结论.
解:(1)设反比例函数的解析式为y=(k≠0),
∵反比例函数图象经过点A(﹣4,﹣2),
∴﹣2=![]() ,解得k=8,
,解得k=8,
∴反比例函数的解析式为y=.
∵B(a,4)在y=的图象上,
∴4=,
∴a=2,
∴点B的坐标为B(2,4);
设一次函数表达式为y=mx+n,将点A,点B代入得,![]() ,解得
,解得![]() ,
,
∴一次函数表达式为y=x+2;
(2)根据图象得,当x>2或﹣4<x<0时,一次函数的值大于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.

(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是
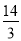 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据: 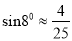 ,
,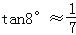 ,
, 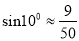 ,
, 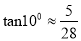 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)有四张背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图).小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.

(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片可用A、B、C、D表示)
(2)求摸出的两张卡片图形都是中心对称图形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,BC⊥AB与点B,连接OC交⊙O于点E,弦AD∥OC.
求证:(1)DE=BE;
(2)CD是⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
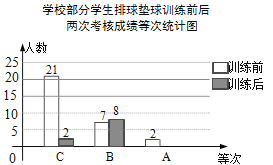
(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某红外线波长为0.00 000 094m,用科学记数法把0.00 000 094m可以写成m.
-
科目: 来源: 题型:
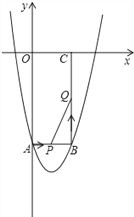
查看答案和解析>>【题目】(12分)如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
相关试题

