【题目】如图,AB为⊙O的直径,BC⊥AB与点B,连接OC交⊙O于点E,弦AD∥OC.
求证:(1)DE=BE;
(2)CD是⊙O的切线.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】【解析】连接OD,由平行可得∠DAO=∠COB,∠ADO=∠DOC;再OA=OD,可得出,∠DAO=∠ADO,则∠COB=∠COD,推出![]() =
=![]() ,从而证出DE=BE.
,从而证出DE=BE.
(2)由(1)得△COD≌△COB,则∠CDO=∠B.又BC⊥AB,则∠CDO=∠B=90°,从而得出CD是 O的切线.

本题解析:证明:(1)连接OD.
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠DOC,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COB=∠COD,
∴![]() =
=![]()
∴ DE=BE
(2)由(1)知∠DOE=∠BOE,
在△COD和△COB中,
CO=CO,
∠DOC=∠BOC,
OD=OB,
∴△COD≌△COB,
∴∠CDO=∠B.
又∵BC⊥AB,
∴∠CDO=∠B=90,即OD⊥CD.
即CD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(m,2)与点Q(3,n)关于x轴对称,则P点关于原点对称的点M的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.

(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是
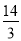 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据: 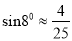 ,
,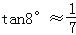 ,
, 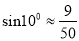 ,
, 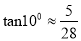 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)有四张背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图).小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.

(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片可用A、B、C、D表示)
(2)求摸出的两张卡片图形都是中心对称图形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).

(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
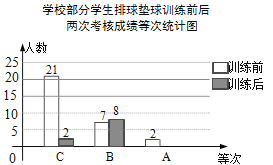
(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某红外线波长为0.00 000 094m,用科学记数法把0.00 000 094m可以写成m.
相关试题

