【题目】数学课上,老师出示了如下的题目:“在等边△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图1,试确定线段AE与DB的大小关系,并说明理由.”小敏与同桌小聪讨论后,进行了如下解答:
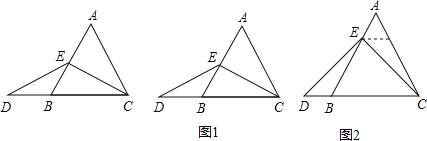
(1)特殊情况,探索结论:当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“≥”,“≤”或“=”)
(2)特例启发,解答题目
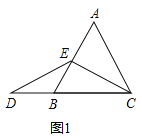
解:题目中,AE与DB的大小关系是:AE DB(填“≥”,“≤”或“=”).理由如下:如图3,过点E做EF∥BC,交AC于点F.(请你完成解答过程)
(3)拓展结论,设计新题.
已知O是等边三角形ABD的边BD的中点,AB=4,EF分别为射线AB、DA上一动点,且∠EOF=120°,若AF=1,求BE的长.
参考答案:
【答案】(1)=;(2)=,(3)3或1.
【解析】
(1)当E为中点时∠D=∠BED=30°即可证明
(2)过E作EF∥BC交AC于点F,证明△DBE≌△EFC,可得BD=EF,从而证明得出
(3)分别讨论当F在线段DA的延长线上,当F点在线段DA上时,证明△OMF≌△OBE,BE=MF即可求出
解:(1)如图1中,
∵△ABC是等边三角形,AE=EB,
∴∠BCE=∠ACE=30°,∠ABC=60°,
∵ED=EC,
∴∠D=∠ECD=30°,
∵∠EBC=∠D+∠BED,
∴∠D=∠BED=30°,
∴BD=BE=AE.
故答案为=.
(2)结论:AE=BD.理由如下:
如图2中,作EF∥BC交AC于F.
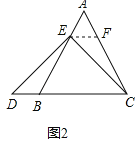
∵∠AEF=∠B=60°,∠A=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,∠AFE=60°,
∴∠EFC=∠DBE=120°,
∵AB=AC,AE=AF,
∴BE=CF,
∵∠D=∠ECB=∠CEF,
在△DBE和△FEC中,
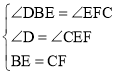 ,
,
∴△DBE≌△EFC,
∴BD=EF=AE,
∴BD=AE,
故答案为=.
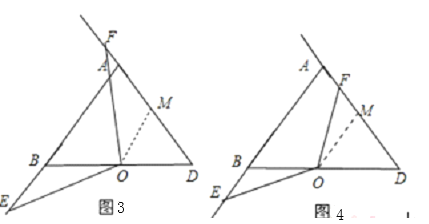
(3)当F在线段DA的延长线上,如图3,作OM∥AB交AD于M,
∵O为等边△ABD的边BD的中点,
∴OB=2,∠D=∠ABC=60°,
∴△ODM为等边三角形,
∴OM=MD=2,∠OMD=60°,
∴FM=FA+AM=3,∠FMO=∠BOM=120°,
∵∠EOF=120゜,
∴∠BOE=∠FOM,
而∠EBO=180°-∠ABC=120°,
在△OMF和△OBE中,
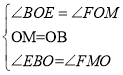 ,
,
∴△OMF≌△OBE,
∴BE=MF=3;
当F点在线段DA上,如图4,
∵O为等边△ABD的边BD的中点,
∴OB=2,∠D=∠ABC=60°,
∴△ODM为等边三角形,
∴OM=MD=2,∠OMD=60°,
∴FM=AM-FA=1,∠FMO=∠BOM=120°,
∵∠EOF=120゜,
∴∠BOE=∠FOM,
而∠EBO=180°-∠ABC=120°,
在△OMF和△OBE中,
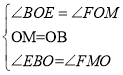 ,
,
∴△OMF≌△OBE,
∴BE=MF=1;
所以BE的值为3或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间
 用t表示,单位:小时
用t表示,单位:小时 ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按 ,
, ,
, ,
, 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
 求本次调查的学生人数;
求本次调查的学生人数; 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整; 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足 的人数.
的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第
 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含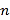 的式子表示)
的式子表示)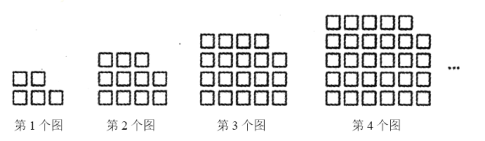
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知蜗牛从
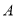 点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:
点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位: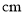 )依次为:+7,-5,-10,-8,+9,-6,+12,+4.
)依次为:+7,-5,-10,-8,+9,-6,+12,+4.(1)若
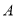 点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;
点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;(2)蜗牛在(1)题在数轴上停的位置作以下运动:第1次向左移动1个单位长度至
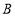 点,第2次从
点,第2次从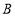 点向右移动2个单位长度至
点向右移动2个单位长度至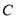 点,第3次从
点,第3次从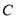 点向左移动3个单位长度至
点向左移动3个单位长度至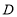 点,第4次从
点,第4次从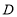 点向右移动4个单位长度至
点向右移动4个单位长度至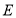 点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案).
点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点
 距离等于
距离等于 的点的轨迹是以点
的点的轨迹是以点 为圆心,半径长为
为圆心,半径长为 的圆
的圆C.到直线
 距离等于
距离等于 的点的轨迹是两条平行于
的点的轨迹是两条平行于 且与
且与 的距离等于
的距离等于 的直线
的直线D.等腰三角形
 的底边
的底边 固定,顶点
固定,顶点 的轨迹是线段
的轨迹是线段 的垂直平分线
的垂直平分线 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元
 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同. 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价; 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
相关试题

