搜索
【题目】某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元
已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同．
求甲、乙两种商品的每件进价；
该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为60元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变要使两种商品全部售完后共获利不少于2460元，问甲种商品按原销售单价至少销售多少件？
参考答案：
【答案】
甲种商品的每件进价为40元，乙种商品的每件进价为48元；
甲种商品按原销售单价至少销售20件．
【解析】设甲种商品的每件进价为x元，乙种商品的每件进价为（x+8）)元
根据“某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元购进的甲、乙两种商品件数相同”列出方程进行求解即可；
设甲种商品按原销售单价销售a件，则由“两种商品全部售完后共获利不少于2460元”列出不等式进行求解即可．
设甲种商品的每件进价为x元，则乙种商品的每件进价为
元，
根据题意得，
，
解得
，
经检验，是原方程的解，
答：甲种商品的每件进价为40元，乙种商品的每件进价为48元；
甲乙两种商品的销售量为
，
设甲种商品按原销售单价销售a件，则
，
解得
，
答：甲种商品按原销售单价至少销售20件．
-
科目： 来源： 题型：
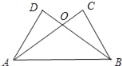
查看答案和解析>>【题目】如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：△OAB是等腰三角形．
-
科目： 来源： 题型：
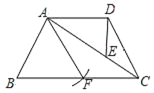
查看答案和解析>>【题目】如图，已知梯形ABCD中，AD∥BC，AB=CD，点E在对角线AC上，且满足∠ADE=∠BAC．
（1）求证：CDAE=DEBC；
（2）以点A为圆心，AB长为半径画弧交边BC于点F，联结AF．求证：AF2=CECA．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直角△ABC的三个顶点分别是A（﹣3，1），B（0，3），C（0，1）
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1；
（2）分别连结AB1、BA1后，求四边形AB1A1B的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为
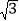，点E、F分别为边AD、CD上一点，将正方形分别沿BE、BF折叠，点A的对应点M恰好落在BF上，点C的对应点N恰好落在BE上，则图中阴影部分的面积为_________．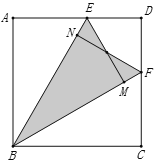
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，图1中ΔABC是等边三角形，DE是中位线，F是线段BC延长线上一点，且CF=AE，连接BE，EF.
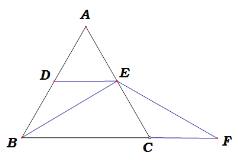
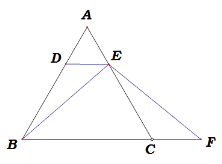
图1 图2
(1)求证：BE=EF；
(2)若将DE从中位线的位置向上平移，使点D、E分别在线段AB、AC上(点E与点A不重合)，其他条件不变，如图2，则(1)题中的结论是否成立？若成立,请证明；若不成立.请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：小丁在研究数学问题时遇到一个定义：对于排好顺序的三个数：x1，x2，x3，称为数列x1，x2，x3，计算
，
，
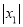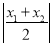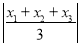，将这三个数的最小值称为数列x1，x2，x3的价值.例如，对于数列2，-1，3，因为
，
，
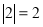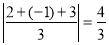，所以数列2，-1，3的价值为
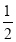.小丁进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值.如数列-1，2，3的价值为
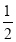；数列3，-1，2的价值为1：…经过研究，小丁发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为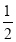.根据以上材料，回答下列问题：(1)数列4，3，-2的价值为______.
(2)将“4，3，-2”这三个数按照不同的顺序排列，可得到若干个数列，求这些数列的价值的最小值(请写出过程并作答).
(3)将3，-8，a(a>1)这三个数按照不同的顺序排列，可得到若干个数列.若这些数列的价值的最小值为1，则a的值为_______ (直接写出答案).
相关试题
