【题目】如图,在平面直角坐标系中,A、B坐标分别为A(0,a)、B(b,a),且a,b满足:(a-3)2+![]() =0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
=0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.

(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在点M,连接MC、MD,使S△MCD=四边形ABDC?若存在这样的点,求出点M的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA、PO,当点P在BD上移动时(不与B、D重合),![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
参考答案:
【答案】(1)S四边形ABDC=15;(2)存在点M(0,6)或(0,-6),使S△MCD=S四边形ABDC ,见解析;(3)不变,见解析.
【解析】
(1)由偶次方及算术平方根的非负性可求出a、b的值,进而即可得出点A、B的坐标,再根据平移的性质可得出点C、D的坐标以及四边形ABDC为平行四边形,套用平行四边形的面积公式即可求出四边形ABDC的面积;
(2)设存在点M(0,y),根据三角形的面积结合S△MCD=S四边形ABDC,即可得出关于y的含绝对值符号的一元一次方程,解之即可得出结论;
(3)过P点作PE∥AB交OC与E点,根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值为1.
解:(1)∵(a-3)2+![]() =0,
=0,
∴a=3,b=5,
∴点A(0,3),B(5,3).
将点A,B分别向下平移3个单位,再向左平移1个单位,得到点C、D,
∴点C(-1,0),D(4,0).
由AB平移得出CD可知,AB∥CD,且AB=CD=5,
∴四边形ABDC为平行四边形,
∴S四边形ABDC=5×3=15.
(2)设存在点M(0,y),
根据题意得:S△MCD=![]() ×5|y|=S四边形ABDC=15,
×5|y|=S四边形ABDC=15,
∴![]() ×5|y|=15,解得:y=±6,
×5|y|=15,解得:y=±6,
∴存在点M(0,6)或(0,-6),使S△MCD=S四边形ABDC.
(3)当点P在BD上移动时,![]() =1不变,理由如下:
=1不变,理由如下: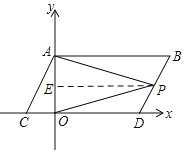
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名
西红柿
豆角
批发价(单位:元/kg)
2.0
1.5
零售价(单位:元/kg)
2.9
2.6
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年6月28日,深湛高铁正式运营.从湛江到广州全程约468km,高铁开通后,运行时间比特快列车所用的时间减少了6h.若高铁列车的平均速度是特快列车平均速度的3倍,求特快列车与高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:

请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】给定一列分式:
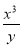 ,
,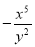 ,
,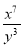 ,
,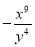 ,…(其中
,…(其中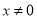 ).
).(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式和第8个分式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用
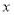 ,
, 表示直角三角形的两直角边
表示直角三角形的两直角边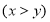 ,下列四个说法:①
,下列四个说法:①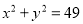 ;②
;②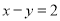 ;③
;③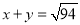 ;④
;④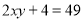 ;其中说法正确的是
;其中说法正确的是
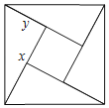
A. ①②B. ①②③C. ①②④D. ①②③④
相关试题

