【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()
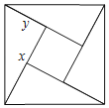
A. ①②B. ①②③C. ①②④D. ①②③④
参考答案:
【答案】D
【解析】
大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49;小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x-y=2;其中④由2xy+4=49可得2xy=45①,又由x2+y2=49②,可得![]() ;还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即
;还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即![]() ,化简得④2xy+4=49;从而求解.
,化简得④2xy+4=49;从而求解.
解:如图
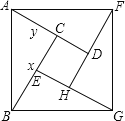
①![]() 为直角三角形,
为直角三角形,
![]() 根据勾股定理:
根据勾股定理:![]() ,
,
故本选项正确;
②由图可知,![]() ,
,
故本选项正确;
③由![]() 可得
可得![]() ①,
①,
又![]() ②,
②,
![]() ①
①![]() ②得,
②得,![]() ,
,
整理得,![]() ,
,
![]() ,
,
故本选项正确.
④由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,列出等式为![]() ,
,
即![]() ;
;
故本选项正确;
![]() 正确结论有①②③④.
正确结论有①②③④.
故选:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B坐标分别为A(0,a)、B(b,a),且a,b满足:(a-3)2+
 =0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
=0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在点M,连接MC、MD,使S△MCD=四边形ABDC?若存在这样的点,求出点M的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA、PO,当点P在BD上移动时(不与B、D重合),
 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】给定一列分式:
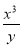 ,
,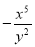 ,
,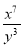 ,
,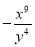 ,…(其中
,…(其中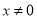 ).
).(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式和第8个分式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
完成作业
单元测试
期末考试
小张
70
90
80
小王
60
75
(1)若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;
(2)若按完成作业、单元检测、期末考试三项成绩按
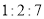 的权重来确定期末评价成绩.
的权重来确定期末评价成绩.①请计算小张的期末评价成绩为多少分?
②小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人同时登山,甲乙两人距地面的高度
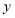 (米
(米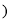 与登山时间
与登山时间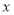 (分
(分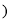 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲登山的速度是 米
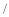 分钟,乙在
分钟,乙在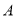 地提速时距地面的高度
地提速时距地面的高度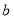 为 米;
为 米;(2)直接写出甲距地面高度
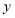 (米
(米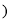 和
和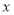 (分
(分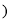 之间的函数关系式;
之间的函数关系式;(3)若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距
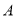 地的高度为多少米?
地的高度为多少米?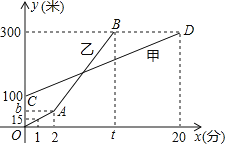
相关试题

