【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
参考答案:
【答案】![]() A、B两种品牌服装每套进价分别为100元、75元;
A、B两种品牌服装每套进价分别为100元、75元;![]() 至少购进A品牌服装的数量是17套
至少购进A品牌服装的数量是17套
【解析】分析:(1)首先设A品牌服装每套进价为x元,则B品牌服装每套进价为(x-25)元,根据关键语句“用2000元购进A种服装数量是用750元购进B种服装数量的2倍.”列出方程,解方程即可;
(2)首先设购进A品牌的服装a套,则购进B品牌服装(2a+4)套,根据“可使总的获利超过1200元”可得不等式(130-100)a+(95-75)(2a+4)>1200,再解不等式即可.
详解:![]() 设A品牌服装每套进价为x元,则B品牌服装每套进价为
设A品牌服装每套进价为x元,则B品牌服装每套进价为![]() 元,由题意得:
元,由题意得:
![]() ,
,
解得:![]() ,
,
经检验:![]() 是原分式方程的解,
是原分式方程的解,
![]() ,
,
答:A、B两种品牌服装每套进价分别为100元、75元;
![]() 设购进A品牌的服装a套,则购进B品牌服装
设购进A品牌的服装a套,则购进B品牌服装![]() 套,由题意得:
套,由题意得:
![]() ,
,
解得:![]() ,
,
答:至少购进A品牌服装的数量是17套.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,过点A、C、D作抛物线y=ax2+bx+c(a≠0),与x轴的另一交点为E,连结CE,点A、B、D的坐标分别为(﹣2,0)、(3,0)、(0,4).
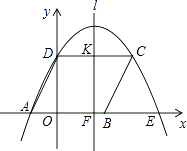
(1)求抛物线的解析式;
(2)已知抛物线的对称轴l交x轴于点F,交线段CD于点K,点M、N分别是直线l和x轴上的动点,连结MN,当线段MN恰好被BC垂直平分时,求点N的坐标;
(3)在满足(2)的条件下,过点M作一条直线,使之将四边形AECD的面积分为3:4的两部分,求出该直线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示,已知MN∥PQ,点B在MN上,点C在PQ上,点A在点B的左侧,点D在点C的右侧,∠ADC,∠ABC的平分线相交于点E(不与B,D点重合),∠CBN=110°.
(1)若∠ADQ=140°,写出∠BED的度数 (直接写出结果即可);
(2)若∠ADQ=m°,将线段AD沿DC方向平移,使点D移动到点C的左侧,其他条件不变,如图②所示,求∠BED的度数(用含m的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程

(1)若方程的增根为x=1,求m的值
(2)若方程有增根,求m的值
(3)若方程无解,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a、b,定义一种运算“”为:ab=a2+ab﹣2,有下列命题: ①13=2;
②方程x1=0的根为:x1=﹣2,x2=1;
③不等式组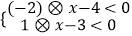 的解集为:﹣1<x<4;
的解集为:﹣1<x<4;
④点( ,
,  )在函数y=x(﹣1)的图象上.
)在函数y=x(﹣1)的图象上.
其中正确的是( )
A.①②③④
B.①③
C.①②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为 .

相关试题

