【题目】如图,四边形ABCD是平行四边形,过点A、C、D作抛物线y=ax2+bx+c(a≠0),与x轴的另一交点为E,连结CE,点A、B、D的坐标分别为(﹣2,0)、(3,0)、(0,4).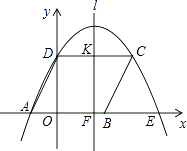
(1)求抛物线的解析式;
(2)已知抛物线的对称轴l交x轴于点F,交线段CD于点K,点M、N分别是直线l和x轴上的动点,连结MN,当线段MN恰好被BC垂直平分时,求点N的坐标;
(3)在满足(2)的条件下,过点M作一条直线,使之将四边形AECD的面积分为3:4的两部分,求出该直线的解析式.
参考答案:
【答案】
(1)
解:∵点A、B、D的坐标分别为(﹣2,0)、(3,0)、(0,4),且四边形ABCD是平行四边形,
∴AB=CD=5,
∴点C的坐标为(5,4),
∵过点A、C、D作抛物线y=ax2+bx+c(a≠0),
∴ 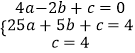 ,
,
解得 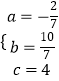 .
.
故抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
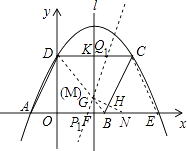
(2)
解:连结BD交对称轴于G,
在Rt△OBD中,易求BD=5,
∴CD=BD,则∠DCB=∠DBC,
又∵∠DCB=∠CBE,
∴∠DBC=∠CBE,
过G作GN⊥BC于H,交x轴于N,
易证GH=HN,
∴点G与点M重合,
故直线BD的解析式y=﹣ ![]() x+4
x+4
根据抛物线可知对称轴方程为x= ![]() ,
,
则点M的坐标为( ![]() ,
, ![]() ),即GF=
),即GF= ![]() ,BF=
,BF= ![]() ,
,
∴BM= ![]() =
= ![]() ,
,
又∵MN被BC垂直平分,
∴BM=BN= ![]() ,
,
∴点N的坐标为( ![]() ,0)
,0)
(3)
解:过点M作直线交x轴于点P1,连结CE.
易求四边形AECD的面积为28,四边形ABCD的面积为20,
由“四边形AECD的面积分为3:4”可知直线P1M必与线段CD相交,
设交点为Q1,四边形AP1Q1D的面积为S1,四边形P1ECQ1的面积为S2,点P1的坐标为(a,0),
假设点P在对称轴的左侧,则P1F= ![]() ﹣a,P1E=7﹣a,
﹣a,P1E=7﹣a,
由△MKQ1∽△MFP1,得 ![]() =
= ![]() ,
,
易求Q1K=5P1F=5( ![]() ﹣a),
﹣a),
∴CQ1= ![]() ﹣5(
﹣5( ![]() ﹣a)=5a﹣10,
﹣a)=5a﹣10,
∴S2= ![]() (5a﹣10+7﹣a)×4=28×
(5a﹣10+7﹣a)×4=28× ![]() ,
,
解得:a= ![]() ,
,
根据P1( ![]() ,0),M(
,0),M( ![]() ,
, ![]() )可求直线P1M的解析式为y=
)可求直线P1M的解析式为y= ![]() x﹣6,
x﹣6,
若点P在对称轴的右侧,则直线P2M的解析式为y=﹣ ![]() x+
x+ ![]()
【解析】(1)根据平行四边形的性质可求点C的坐标,由待定系数法即可求出抛物线的解析式;(2)连结BD交对称轴于G,过G作GN⊥BC于H,交x轴于N,根据待定系数法即可求出直线BD的解析式,根据抛物线对称轴公式可求对称轴,由此即可求出点N的坐标;(3)过点M作直线交x轴于点P1 , 分点P在对称轴的左侧,点P在对称轴的右侧,两种情况讨论即可求出直线的解析式.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.

(1)当日本渔船受到严重警告信号后,必须沿北偏东转向多少度航行,才能恰好避免进入钓鱼岛12海里禁区?
(2)当日本渔船不听严重警告信号,仍按原速度,原方向继续前进,那么海监船必须尽快到达距岛12海里,且位于线段AC上的F处强制拦截渔船,问海监船能否比日本渔船先到达F处?(注:①中国海监船的最大航速为18节,1节=1海里/小时;②参考数据:sin26.3°≈0.44,sin20.5°≈0.35,sin18.1°≈0.31,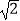 ≈1.4,
≈1.4, 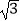 ≈1.7)
≈1.7) -
科目: 来源: 题型:
查看答案和解析>>【题目】横坐标和纵坐标都是整数的点叫作整点,函数y=
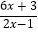 的图象上的整点的个数是( )
的图象上的整点的个数是( )A. 3个 B. 4个 C. 6个 D. 8个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.

(1)如图1,当点M与点C重合,求证:DF=MN;
(2)如图2,假设点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以 cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);
①判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
②连结FM、FN,△MNF能否为等腰三角形?若能,请写出a,t之间的关系;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示,已知MN∥PQ,点B在MN上,点C在PQ上,点A在点B的左侧,点D在点C的右侧,∠ADC,∠ABC的平分线相交于点E(不与B,D点重合),∠CBN=110°.
(1)若∠ADQ=140°,写出∠BED的度数 (直接写出结果即可);
(2)若∠ADQ=m°,将线段AD沿DC方向平移,使点D移动到点C的左侧,其他条件不变,如图②所示,求∠BED的度数(用含m的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程

(1)若方程的增根为x=1,求m的值
(2)若方程有增根,求m的值
(3)若方程无解,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六
 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍. 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元? 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
相关试题

