【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

参考答案:
【答案】(1)作图见解析;(2)作图见解析;(3)45°.
【解析】
(1)、将点A、B、C分别右移2个单位、下移2个单位得到其对应点,顺次连接即可得;(2)、分别作出点D、E、F关于直线l的对称点,顺次连接即可得;(3)、连接A′F′,利用勾股定理逆定理证△A′C′F′为等腰直角三角形即可得.
(1)△A′B′C′即为所求;
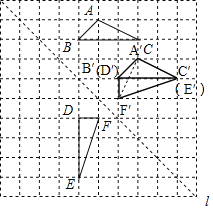
(2)△D′E′F′即为所求;
(3)如图,连接A′F′, ∵△ABC≌△A′B′C′、△DEF≌△D′E′F′,
∴∠C+∠E=∠A′C′B′+∠D′E′F′=∠A′C′F′,
∵A′C′=![]() ,A′F′=
,A′F′=![]() ,C′F′=
,C′F′=![]() ,
,
∴A′C′2+A′F′2=5+5=10=C′F′2, ∴△A′C′F′为等腰直角三角形,
∴∠C+∠E=∠A′C′F′=45°,
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差
(单位:千克)



1
2
箱数
2
6
10
8
4
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)已知:
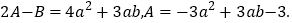
(1)求
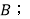 (用含
(用含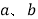 的代数式表示)
的代数式表示)(2)比较
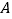 与
与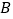 的大小
的大小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式的规律,解答下列问题:
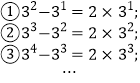
(1)按此规律,第④个等式为_________;第
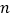 个等式为_______;(用含
个等式为_______;(用含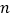 的代数式表示,
的代数式表示,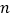 为正整数)
为正整数)(2)按此规律,计算:
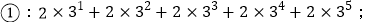
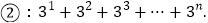
相关试题

