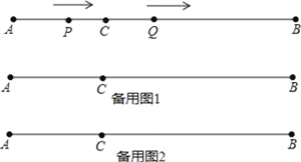
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

参考答案:
【答案】 4 8
【解析】试题分析:(1)由于AB=12cm,点C是线段AB上的一点,BC=2AC,则AC+BC=3AC=AB=12cm,依此即可求解;
(2)分别表示出AP、PQ,然后根据等量关系AP=PQ列出方程求解即可;
(3)分相遇前、相遇后以及到达B点返回后相距1cm四种情况列出方程求解即可.
试题解析:(1)∵AB=12cm,点C是线段AB上的一点,BC=2AC,
∴AC+BC=3AC=AB=12cm,
∴AC=4cm,BC=8cm;
(2)由题意可知:AP=3t,PQ=4﹣(3t﹣t),
则3t=4﹣(3t﹣t),
解得:t=![]() .
.
答:当t=![]() 时,AP=PQ.
时,AP=PQ.
(3)∵点P、Q相距的路程为1cm,
∴(4+t)﹣3t=1(相遇前)或3t﹣(4+t)=1(第一次相遇后),
解得t=![]() 或t=
或t=![]() ,
,
当到达B点时,第一次相遇后点P、Q相距的路程为1cm,
3t+4+t=12+12﹣1
解得:t=![]() .
.
答:当t为![]() ,
, ![]() ,
, ![]() 时,PQ=1cm.
时,PQ=1cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=
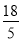 ,sin∠BAM=
,sin∠BAM= ,求线段AM的长.
,求线段AM的长.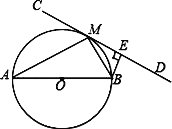
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在A,E的异侧,BD⊥AE于D,CE⊥AE于E
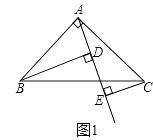
(1)试说明:BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果;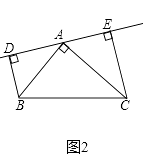
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需说明理由.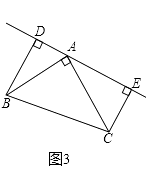
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列单项式:﹣x2 , 3x3 , ﹣5x4 , 7x5 , …,按此规律排列,则第7个单项式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2y+xy2)﹣2(x2y﹣x)﹣2xy2﹣2y,其中x=﹣2,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知:(x﹣3)2+|y+
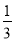 |=0,求3x2y﹣[2xy2﹣2(xy
|=0,求3x2y﹣[2xy2﹣2(xy 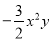 )+3xy]+5xy2的值.
)+3xy]+5xy2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在同一直线上,且AB:BC:CD=2:3:5
(1)若AD=24cm,求AB、BC、CD的长;
(2)若点M、N是AC、CD中点,且AD=a,求MN的长.

相关试题

