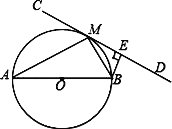
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)8.
【解析】试题分析:(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,
(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
试题解析:(1)如图,连接OM,
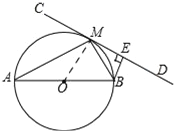
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB;
(2)由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴![]()
∴BM2=BEAB;
(3)由(1)有,∠BME=∠MAB,
∵sin∠BAM=![]() ,
,
∴sin∠BME=![]() ,
,
在Rt△BEM中,BE=![]() ,
,
∴sin∠BME=![]() =
=![]() ,
,
∴BM=6,
在Rt△ABM中,sin∠BAM=![]() ,
,
∴sin∠BAM=![]() =
=![]() ,
,
∴AB=![]() BM=10,据勾股定理得,AM=8.
BM=10,据勾股定理得,AM=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】投影线垂直于投影面产生的投影叫做______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,DE∥BC.
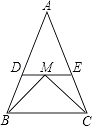
(1)试问△ADE是否是等腰三角形,说明理由;
(2)若M为DE上的点,且BM平分∠ABC,CM平分∠ACB,若△ADE的周长为20,BC=8.求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3x(x﹣1)﹣2(x﹣1)
(2)3x2﹣12x+12. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在A,E的异侧,BD⊥AE于D,CE⊥AE于E
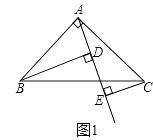
(1)试说明:BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果;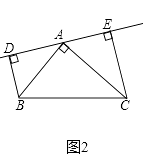
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需说明理由.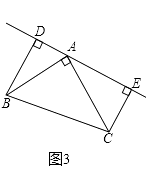
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列单项式:﹣x2 , 3x3 , ﹣5x4 , 7x5 , …,按此规律排列,则第7个单项式为 .
-
科目: 来源: 题型:
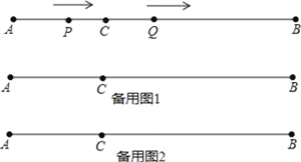
查看答案和解析>>【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

相关试题

