【题目】如图,点A、B、C、D在同一直线上,且AB:BC:CD=2:3:5
(1)若AD=24cm,求AB、BC、CD的长;
(2)若点M、N是AC、CD中点,且AD=a,求MN的长.
![]()
参考答案:
【答案】(1)AB=4.8cm;BC=7.2cm;CD =12cm;(2)![]()
【解析】试题分析(1)求出AB=![]() AD,BC=
AD,BC=![]() AD,CD=
AD,CD=![]() AD,代入求出即可;
AD,代入求出即可;
(2)根据线段中点的定义得出CM=![]() AC,CN=
AC,CN=![]() CD,求出MN=
CD,求出MN=![]() AD,代入求出即可.
AD,代入求出即可.
试题解析:(1)∵AB:BC:CD=2:3:5,AD=24cm,
∴AB=![]() AD=
AD=![]() ×24cm=4.8cm;
×24cm=4.8cm;
BC=![]() AD=
AD=![]() ×24cm=7.2cm;
×24cm=7.2cm;
CD=![]() AD=12cm;
AD=12cm;
(2)∵点M、N是AC、CD中点,
![]()
∴CM=![]() AC,CN=
AC,CN=![]() CD,
CD,
∵AD=a,
∴MN=CM+CN=![]() AC+
AC+![]() CD=
CD=![]() AD=
AD=![]() a.
a.
-
科目: 来源: 题型:
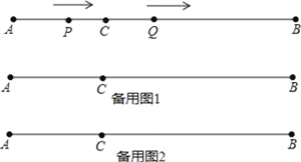
查看答案和解析>>【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2y+xy2)﹣2(x2y﹣x)﹣2xy2﹣2y,其中x=﹣2,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知:(x﹣3)2+|y+
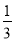 |=0,求3x2y﹣[2xy2﹣2(xy
|=0,求3x2y﹣[2xy2﹣2(xy 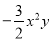 )+3xy]+5xy2的值.
)+3xy]+5xy2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2016)2+2017的顶点坐标是( )
A.(2016,﹣2017)
B.(﹣2016,2017)
C.(2016,2017)
D.(﹣2016,﹣2017) -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣2(x﹣3)2+4的顶点坐标是( )
A.(3,4)B.(﹣3,4)C.(3,﹣4)D.(﹣3,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店将某种服装按成本价提高40%标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的成本多少元?
相关试题

