【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】解:由图知: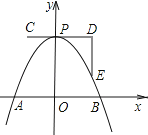
当点B的横坐标为1时,抛物线顶点取C(﹣1,4),设该抛物线的解析式为:y=a(x+1)2+4,代入点B坐标,得:
0=a(1+1)2+4,a=﹣1,
即:B点横坐标取最小值时,抛物线的解析式为:y=﹣(x+1)2+4.
当A点横坐标取最大值时,抛物线顶点应取E(3,1),则此时抛物线的解析式:y=﹣(x﹣3)2+1=﹣x2+6x﹣8=﹣(x﹣2)(x﹣4),即与x轴的交点为(2,0)或(4,0)(舍去),
∴点A的横坐标的最大值为2.
故选B.
抛物线在平移过程中形状没有发生变化,因此函数解析式的二次项系数在平移前后不会改变.首先,当点B横坐标取最小值时,函数的顶点在C点,根据待定系数法可确定抛物线的解析式;而点A横坐标取最大值时,抛物线的顶点应移动到E点,结合前面求出的二次项系数以及E点坐标可确定此时抛物线的解析式,进一步能求出此时点A的坐标,即点A的横坐标最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:
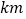 )依先后次序记录如下:
)依先后次序记录如下: ,
,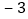 ,
,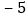 ,
,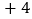 ,
,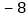 ,
,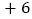 ,
,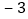 ,
,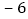 ,
,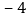 ,
,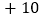 .
.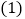 将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?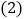 出租车在行驶过程中,离鼓楼最远的距离是多少?
出租车在行驶过程中,离鼓楼最远的距离是多少?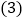 出租车按物价部门规定,起步价(不超过
出租车按物价部门规定,起步价(不超过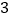 千米)为
千米)为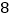 元,超过
元,超过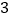 千米的部分每千米的价格为
千米的部分每千米的价格为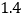 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】先观察表格,再解决问题.
项数
第一项
前两项
前三项
前四项
前五项
式子①

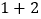
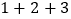
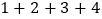
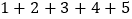
式子②
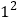


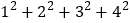
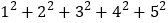
两个式子的比




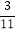
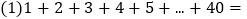 ________(直接写出结果);
________(直接写出结果);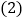 计算
计算 的值;
的值;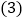 计算
计算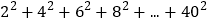 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上
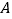 ,
,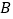 两点对应的数分别为
两点对应的数分别为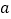 ,
,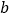 ,且满足
,且满足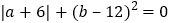 ;
; 求
求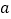 ,
,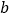 的值;
的值; 若点
若点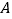 以每秒
以每秒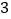 个单位,点
个单位,点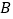 以每秒
以每秒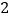 个单位的速度同时出发向右运动,多长时间后
个单位的速度同时出发向右运动,多长时间后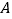 ,
,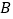 两点相距
两点相距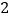 个单位长度?
个单位长度? 已知
已知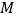 从
从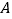 向右出发,速度为每秒一个单位长度,同时
向右出发,速度为每秒一个单位长度,同时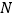 从
从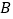 向右出发,速度为每秒
向右出发,速度为每秒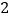 个单位长度,设
个单位长度,设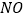 的中点为
的中点为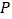 ,
, 的值是否变化?若不变求其值;否则说明理由.
的值是否变化?若不变求其值;否则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的集合中:
—7 , 0,
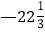 , —2.55555……, 3.01, +9 , 4.020020002…, +10﹪,
, —2.55555……, 3.01, +9 , 4.020020002…, +10﹪, 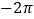
有理数集合:{ };
无理数集合:{ };
整数集合:{ };
分数集合:{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.

(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
相关试题

