【题目】数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() ,
,![]() ,且满足
,且满足![]() ;
;
![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 若点
若点![]() 以每秒
以每秒![]() 个单位,点
个单位,点![]() 以每秒
以每秒![]() 个单位的速度同时出发向右运动,多长时间后
个单位的速度同时出发向右运动,多长时间后![]() ,
,![]() 两点相距
两点相距![]() 个单位长度?
个单位长度?
![]() 已知
已知![]() 从
从![]() 向右出发,速度为每秒一个单位长度,同时
向右出发,速度为每秒一个单位长度,同时![]() 从
从![]() 向右出发,速度为每秒
向右出发,速度为每秒![]() 个单位长度,设
个单位长度,设![]() 的中点为
的中点为![]() ,
,![]() 的值是否变化?若不变求其值;否则说明理由.
的值是否变化?若不变求其值;否则说明理由.
参考答案:
【答案】![]()
![]() ,
,![]() ;
; ![]()
![]() 秒或
秒或![]() 秒后
秒后![]() ,
,![]() 两点相距
两点相距![]() 个单位长度;
个单位长度; ![]()
![]() 为定值
为定值![]() .
.
【解析】
(1)根据绝对值以及偶次方的非负性即可得出关于a、b的一元一次方程,解之即可得出a、b的值;
(2)设x秒后A,B两点相距2个单位长度,根据点A、B的运动找出x秒后点A、B对应的数,再根据两点相距2个单位长度即可得出关于x的含绝对值符号的一元一次方程,解之即可得出结论;
(3)找出当运动时间为t秒时,点M、N对应的数,结合NO的中点为P即可找出PO、AM,二者做差后即可得出结论.
(1)∵|a+6|+(b﹣12)2=0,∴a+6=0,b﹣12=0,∴a=﹣6,b=12.
(2)设x秒后A,B两点相距2个单位长度,根据题意得:|(2x+12)﹣(3x﹣6)|=2,解得:x1=16,x2=20.
答:16秒或20秒后A,B两点相距2个单位长度.
(3)当运动时间为t秒时,点M对应的数为t﹣6,点N对应的数为2t+12.
∵NO的中点为P,∴PO=![]() NO=t+6,AM=t﹣6﹣(﹣6)=t,∴PO﹣AM=t+6﹣t=6,∴PO﹣AM为定值6.
NO=t+6,AM=t﹣6﹣(﹣6)=t,∴PO﹣AM=t+6﹣t=6,∴PO﹣AM为定值6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先观察表格,再解决问题.
项数
第一项
前两项
前三项
前四项
前五项
式子①

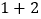
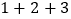
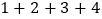
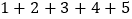
式子②
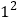


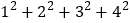
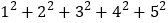
两个式子的比




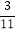
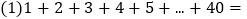 ________(直接写出结果);
________(直接写出结果);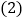 计算
计算 的值;
的值;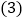 计算
计算 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的集合中:
—7 , 0,
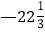 , —2.55555……, 3.01, +9 , 4.020020002…, +10﹪,
, —2.55555……, 3.01, +9 , 4.020020002…, +10﹪, 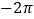
有理数集合:{ };
无理数集合:{ };
整数集合:{ };
分数集合:{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.

(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1,x2,x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( )

A. x1>x2>x3 B. x1>x3>x2 C. x2>x3>x1 D. x3>x2>x1
相关试题

