【题目】如图1,在直角坐标系xoy中,点A、B分别在x、y轴的正半轴上,将线段AB绕点B顺时针旋转90°,点A的对应点为点C.

(1)若A(6,0),B(0,4),求点C的坐标;
(2)以B为直角顶点,以AB和OB为直角边分别在第一、二象限作等腰Rt△ABD和等腰Rt△OBE,连DE交y轴于点M,当点A和点B分别在x、y轴的正半轴上运动时,判断并证明AO与MB的数量关系.
参考答案:
【答案】(1)C(-4,-2);(2)AO= 2MB.证明见解析.
【解析】
(1)过C点作y轴的垂线段,垂足为H点,证明△ABO≌△BCH,利用全等三角形的性质结合C在第三象限即可求得C点坐标;
(2)过D点作DN⊥y轴于点N,证明△DBN≌△BAO,根据全等三角形对应边相等BN=AO,DN=BO,再证明△DMN≌△EMB,可得MN=MB,于是可得AO=2MB.
(1)解:过C点作y轴的垂线段,垂足为H点.

∴∠BHC=∠AOB=90°,
∵A(6,0),B(0,4)
∴OA=6,OB=4
∵∠ABC=90°,
∴∠ABO+∠OBC=90°,又∠ABO+∠OAB=90°,
∴∠OBC=∠OAB,
∵在△ABO和△BCH中
∴△ABO≌△BCH,
∴AO=BH=6,CH=BO=4,
∴OH=2,
∴C(-4,-2).
(2)AO= 2MB.
过D点作DN⊥y轴于点N,

∴∠BND=∠AOB=90°,
∵△ABD、△OBE为等腰直角三角形,
∴∠ABD=∠OBE=90°,AB=BD,BO=BE,
∴∠DBN+∠ABO=∠BAO+∠ABO=90°,
∴∠DBN=∠BAO,
∴△DBN≌△BAO,
∴BN=AO,DN=BO,
在△DMN和△EMB中,
∵DN=BO=BE,∠DNM=∠EBM,∠DMN=∠EMB,
∴△DMN≌△EMB,
∴MN=MB=![]() BN=
BN=![]() AO
AO
∴AO=2MB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400 m,先到终点的人在终点休息等候对方.已知甲先出发4 min,在整个步行过程中,甲、乙两人的距离y m与甲出发的时间tmin之间的函数关系如图所示.

(1)甲步行的速度为 m/min;
(2)解释点P(16,0)的实际意义;
(3)乙走完全程用了多少分钟?
(4)乙到达终点时,甲离终点还有多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
(1)转动一次转盘,获得50元、30元、10元购物券的概率分别是多少?
(2)如果有一名顾客在商场消费了200元,通过计算说明转转盘和直接获得购物券,哪种方式对这位顾客更合算?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一只口袋里放着
 个红球、
个红球、 个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀. 取出红球的概率为
取出红球的概率为 ,白球有多少个?
,白球有多少个? 取出黑球的概率是多少?
取出黑球的概率是多少? 再在原来的袋中放进多少个红球,能使取出红球的概率达到
再在原来的袋中放进多少个红球,能使取出红球的概率达到 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】用函数方法研究动点到定点的距离问题.
在研究一个动点P(x,0)到定点A(1,0)的距离S时,小明发现:
S与x的函数关系为S=
 并画出图像如图:
并画出图像如图:
借助小明的研究经验,解决下列问题:
(1)写出动点P(x,0)到定点B(-2,0)的距离S的函数表达式,并求当x取何值时,S取最小值?
(2)设动点P(x,0)到两个定点M(1,0)、N(5,0)的距离和为y.
①随着x增大,y怎样变化?
②当x取何值时,y取最小值,y的最小值是多少?
③当x<1时,证明y随着x增大而变化的规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点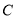 在边
在边 上,且
上,且 ,点
,点 为
为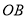 的中点,点
的中点,点 为边
为边 上的动点,当点
上的动点,当点 在
在 上移动时,使四边形
上移动时,使四边形 周长最小的点
周长最小的点 的坐标为( )
的坐标为( )
A.
 B.
B. C.
C. D.
D.
相关试题

