【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
参考答案:
【答案】(1) ![]() ;(2) 转盘的方式更合算,理由见解析
;(2) 转盘的方式更合算,理由见解析
【解析】试题分析:(1)利用大量试验下的频率即为概率,进而求出即可;
(2)算出转一次转盘得到金额的平均数,与10比较即可.
试题解析:解:(1)P(不获奖)=![]() =
=![]() (或65%);
(或65%);
(2)∵转转盘的平均收益为:100×![]() +50×
+50×![]() +20×
+20×![]() =14>10,∴转转盘的方式更合算.
=14>10,∴转转盘的方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的周长是200,其中一条对角线长60.
(1)求另一条对角线的长度.
(2)求菱形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形B.等边三角形C.菱形D.正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的矩形纸片,剪去一个最大的正方形,余下一个四边形,称为第一次操作,在余下的矩形纸片中再剪去一个最大的正方形,余下一个四边形,称为第二次操作,……依次类推,若第n次余下的四边形是正方形,则称原矩形为n阶方形,如图,矩形ABCD中,若AB=1,BC=2,则矩形ABCD为1阶方形.

(1)判断:邻边长分别为2和3的矩形是____阶方形;邻边长分别为3和4的矩形是____阶方形;
(2)已知矩形ABCD是3阶方形,其边长分别为1和a(a﹥1),请画出矩形ABCD及裁剪线的示意图,并在下方写出的a值;
(3)已知矩形ABCD的邻边长分别为a,b(a﹥b),满足a=5b+r,b=4r,请直接写出矩形ABCD是几阶方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m,n满足m﹣n2=1,则代数式m2+2n2+4m﹣1的最小值等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
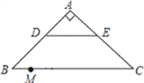
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“爱我海珠,创卫同行”的活动,倡议学生利用双休日在海珠湿地公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:

(1)将条形统计图补充完整.
(2)抽查的学生劳动时间的众数为 , 中位数为 .
(3)已知全校学生人数为1200人,请你估算该校学生参加义务劳动1小时的有多少人?
相关试题

