【题目】用函数方法研究动点到定点的距离问题.
在研究一个动点P(x,0)到定点A(1,0)的距离S时,小明发现:
S与x的函数关系为S= 并画出图像如图:
并画出图像如图:

借助小明的研究经验,解决下列问题:
(1)写出动点P(x,0)到定点B(-2,0)的距离S的函数表达式,并求当x取何值时,S取最小值?
(2)设动点P(x,0)到两个定点M(1,0)、N(5,0)的距离和为y.
①随着x增大,y怎样变化?
②当x取何值时,y取最小值,y的最小值是多少?
③当x<1时,证明y随着x增大而变化的规律.
参考答案:
【答案】(1)S= ,当x=-2时,S的最小值为0;(2)①当x<1时,y随x增大而减小;当1≤x≤5时,y是一个固定的值;当x>5时,y随x增大而增大,②当1≤x≤5时,y取最小值,y的最小值是4,③当x<1时,y随x增大而减小.
,当x=-2时,S的最小值为0;(2)①当x<1时,y随x增大而减小;当1≤x≤5时,y是一个固定的值;当x>5时,y随x增大而增大,②当1≤x≤5时,y取最小值,y的最小值是4,③当x<1时,y随x增大而减小.
【解析】
(1)根据x轴上两点之间的距离等于它们差的绝对值,以及绝对值的意义可直接写出结论;
(2)根据x轴上两点之间的距离等于它们差的绝对值,得出PM和PN的距离,它们之和即为y.①分情况讨论,根据一次函数的性质可得y的变化情况;②根据y的变化情况可求;③当x<1时,![]() ,根据函数的增减性可得.
,根据函数的增减性可得.
(1)S= ;∵当x<2时y随x增大而减小,当x>2时y随x的增大而增大,∴当x=-2时,S的最小值为0.
;∵当x<2时y随x增大而减小,当x>2时y随x的增大而增大,∴当x=-2时,S的最小值为0.
(2)由题意得y=![]() +
+![]() ,根据绝对值的意义,
,根据绝对值的意义,
可转化为y=
①当x<1时,y随x增大而减小;
当1≤x≤5时,y是一个固定的值;
当x>5时,y随x增大而增大.
②当1≤x≤5时,y取最小值,y的最小值是4.
③当x<1时,![]() ,∵-2<0
,∵-2<0
∴当x<1时,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
(1)转动一次转盘,获得50元、30元、10元购物券的概率分别是多少?
(2)如果有一名顾客在商场消费了200元,通过计算说明转转盘和直接获得购物券,哪种方式对这位顾客更合算?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xoy中,点A、B分别在x、y轴的正半轴上,将线段AB绕点B顺时针旋转90°,点A的对应点为点C.

(1)若A(6,0),B(0,4),求点C的坐标;
(2)以B为直角顶点,以AB和OB为直角边分别在第一、二象限作等腰Rt△ABD和等腰Rt△OBE,连DE交y轴于点M,当点A和点B分别在x、y轴的正半轴上运动时,判断并证明AO与MB的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只口袋里放着
 个红球、
个红球、 个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀. 取出红球的概率为
取出红球的概率为 ,白球有多少个?
,白球有多少个? 取出黑球的概率是多少?
取出黑球的概率是多少? 再在原来的袋中放进多少个红球,能使取出红球的概率达到
再在原来的袋中放进多少个红球,能使取出红球的概率达到 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 在边
在边 上,且
上,且 ,点
,点 为
为 的中点,点
的中点,点 为边
为边 上的动点,当点
上的动点,当点 在
在 上移动时,使四边形
上移动时,使四边形 周长最小的点
周长最小的点 的坐标为( )
的坐标为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
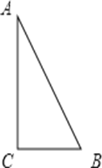
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
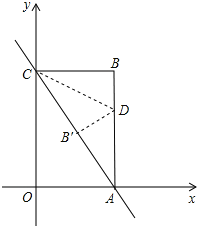
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
相关试题

