【题目】某手机店销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元,销售
元,销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元.
元.
(1)求每部![]() 型手机和
型手机和![]() 型手机的销售利润;
型手机的销售利润;
(2)该手机店计划一次购进![]() ,
,![]() 两种型号的手机共
两种型号的手机共![]() 部,其中
部,其中![]() 型手机的进货量不超过
型手机的进货量不超过![]() 型手机的
型手机的![]() 倍,设购进
倍,设购进![]() 型手机
型手机![]() 部,这
部,这![]() 部手机的销售总利润为
部手机的销售总利润为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②该手机店购进![]() 型、
型、![]() 型手机各多少部,才能使销售总利润最大?
型手机各多少部,才能使销售总利润最大?
(3)在(2)的条件下,该手机店实际进货时,厂家对![]() 型手机出厂价下调
型手机出厂价下调![]() 元,且限定手机店最多购进
元,且限定手机店最多购进![]() 型手机
型手机![]() 部,若手机店保持同种手机的售价不变,设计出使这
部,若手机店保持同种手机的售价不变,设计出使这![]() 部手机销售总利润最大的进货方案.
部手机销售总利润最大的进货方案.
参考答案:
【答案】(1)每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元,每部
元,每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元;(2)①
元;(2)①![]() ;②手机店购进
;②手机店购进![]() 部
部![]() 型手机和
型手机和![]() 部
部![]() 型手机的销售利润最大;(3)手机店购进
型手机的销售利润最大;(3)手机店购进![]() 部
部![]() 型手机和
型手机和![]() 部
部![]() 型手机的销售利润最大.
型手机的销售利润最大.
【解析】
(1)设每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元,每部
元,每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元,根据题意列出方程组求解即可;
元,根据题意列出方程组求解即可;
(2)①根据总利润=销售A型手机的利润+销售B型手机的利润即可列出函数关系式;
②根据题意,得![]() ,解得
,解得![]() ,根据一次函数的增减性可得当当
,根据一次函数的增减性可得当当![]() 时,
时,![]() 取最大值;
取最大值;
(3)根据题意,![]() ,
,![]() ,然后分①当
,然后分①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,三种情况进行讨论求解即可.
时,三种情况进行讨论求解即可.
解:(1)设每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元,每部
元,每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元.
元.
根据题意,得![]() ,
,
解得![]()
答:每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元,每部
元,每部![]() 型手机的销售利润为
型手机的销售利润为![]() 元.
元.
(2)①根据题意,得![]() ,即
,即![]() .
.
②根据题意,得![]() ,解得
,解得![]() .
.
![]() ,
,![]() ,
,
![]() 随
随![]() 的增大而减小.
的增大而减小.
![]() 为正整数,
为正整数,
![]() 当
当![]() 时,
时,![]() 取最大值,
取最大值,![]() .
.
即手机店购进![]() 部
部![]() 型手机和
型手机和![]() 部
部![]() 型手机的销售利润最大.
型手机的销售利润最大.
(3)根据题意,得![]() .
.
即![]() ,
,![]() .
.
①当![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() 取最大值,即手机店购进
取最大值,即手机店购进![]() 部
部![]() 型手机和
型手机和![]() 部
部![]() 型手机的销售利润最大;
型手机的销售利润最大;
②当![]() 时,
时,![]() ,
,![]() ,即手机店购进
,即手机店购进![]() 型手机的数量为满足
型手机的数量为满足![]() 的整数时,获得利润相同;
的整数时,获得利润相同;
③当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() 取得最大值,即手机店购进
取得最大值,即手机店购进![]() 部
部![]() 型手机和
型手机和![]() 部
部![]() 型手机的销售利润最大.
型手机的销售利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知在△ABC中,∠BAC=40°,BD⊥AC于D,CE⊥AB于E,BD、CE所在直线交于点F,求∠BFC的度数;
(2)在(1)的基础上,若∠BAC每秒扩大10°,且在变化过程中∠ABC与∠ACB始终保持是锐角,经过t秒(0<t<14),在∠BFC,∠BAC这两个角中,当一个为另一个的两倍时,求t的值;
(3)在(2)的基础上,∠ABD与∠ACE的角平分线交于点G,∠BGC是否为定值,如果是,请直接写出∠BGC的值,如果不是,请写出∠BGC是如何变化的.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=
 (30°<
(30°<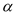 <90°) ,则∠OGA的度数为(用含
<90°) ,则∠OGA的度数为(用含 的代数式表示)____________________.
的代数式表示)____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:
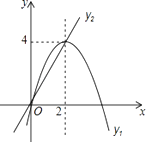
①当0<x<2时,N=y1;
②N随x的增大而增大的取值范围是x<0;
③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;
④若N=2,则x=2﹣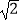 或x=1.
或x=1.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号).①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.
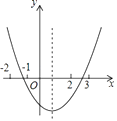
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试说明:(1)直线AB//CD.(2) 如果∠1=55°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.
(1)将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;
(2)连接AA′、CC′,则四边形AA′C′C的面积为 ________.
(3)若连接AA′,BB′,则这两条线段之间的关系是 ;
(4)△ABC的高CD所在直线必经过图中的一个格点点P,在图中标出点P.

相关试题

